





|

 |
В этой работе рассматриваются задачи анализа строк, возникающие при разработке предлагаемой системы обработки текстовой информации. Мы не ставим целью дать точные решения всех возможных задач, а скорее предлагаем обзор существующих алгоритмов, подходящих для подобных системы. Термин анализ строк используется здесь в довольно общем смысле и обозначает целый класс задач – таких, как локализация заданных подстрок, выделение длиннейших совпадающих подстрок двух строк, вычисление расстояния между двумя строками и т.д.
Прежде всего совсем общо описывается проблема, затем приводятся точные формулировки.
Обсуждаются алгоритмы анализа строк, сравниваются их возможности и эффективность. После этого идет описание основных алгоритмов.
Наконец, рассматривается применение этих алгоритмов в предлагаемой системе.
Определения некоторых терминов и обозначений, принятых в этой области, вы найдете в приложениях.
Говоря совсем нестрого, нужно научиться искать образцы, встречающиеся в данной последовательности символов более одного раза. В таком виде формулировка звучит довольно расплывчато, так что отнюдь не лишними будут некоторые уточнения.
Прежде всего, рассматриваемые последовательности – одномерные и составлены из символов. Что это, однако, значит? Из каких символов? Мы можем ограничиться ASCII-литерами, исключив из них пробел (ASCII 33-126), и рассматривать строки (или цепочки, в соответствии с традицией, я буду использовать эти два термина как синонимы – прим.перев.) из этих литер как самостоятельные символы. Тогда упомянутые текстовые последовательности составлены из таких атомарных символов, разделенных пробелами. При этом, однако, совокупность символов оказывается бесконечной. Поэтому, вероятно, проще – и, по-видимому, естественнее – использовать алфавит, объединяющий все уже упомянутые ASCII-литеры, в том числе, и пробел. Последовательностью теперь становится цепочка символов над этим (конечным) алфавитом.
Теперь следует обсудить, что понимается под образцом. Пусть нам нужно искать все имеющиеся повторения внутри заданной строки, чтобы в дальнейшем использовать любую внутреннюю избыточность для разработки подходящей схемы кодирования, что позволит нам увеличить эффективность представления информации. В этом случае образцом может оказаться удобно считать подстроку (она состоит из некоторого числа смежных символов исходной строки). С другой стороны, если требуется проанализировать входную последовательность для выделения синтаксических структур, таких, как периодические зависимости, то образцами удобнее считать подпоследовательности. В любом случае, подстрока является частным случаем подпоследовательности (которая состоит из символов исходной последовательности, стоящих на произвольных местах, но в том же порядке), поэтому для общности образцами будем считать подпоследовательности.
Здесь, пожалуй, следует приостановиться и посмотреть, сколько всего может быть образцов длины k в последовательности длины n. Сначала, рассмотрим подстроки. Из последовательности можно выделить ровно (n - k + 1) подстрок длины k. Общее число подстрок можно вычислить суммированием, что приводит нас к формуле:
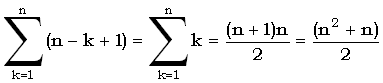
Таким образом, оценкой общего числа подстрок оказывается O(n2).
Обратясь к подпоследовательностям, мы обнаруживаем, что верхняя граница их количества является степенной. Это легко выводится следующим образом. Каждый из символов исходной последовательности находится в одном из двух состояний относительно данной подпоследовательности – он либо входит в нее, либо нет. Отсюда получаем 2n подпоследовательностей, включая пустую строку  .
.
Теперь обсудим, что имелось в виду, когда шла речь о повторяющейся подпоследовательности. Естественно считать, что повторяющиеся экземпляры образца должны полностью различаться, поэтому будут рассматриваться только непересекающиеся повторяющиеся образцы. Например, подпоследовательность AB нельзя считать повторяющейся в последовательности AAB, так как ее элементы не являются непересекающимися – они содержат один и тот же символ B.
Наконец, зная, что число подпоследовательностей в последовательности есть O(2n), легко углядеть, что число непересекающихся повторяющихся подпоследовательностей в худшем случае также экспоненциально. Рассмотрим, например, квадрат длины 2n, т.е. строку x2, где x состоит из n разных символов. (Для конечных алфавитов значение n ограничено мощностью алфавита). Последовательность x2 будет тогда содержать 2n-1 повторяющихся подпоследовательностей, не считая  . Имеется, однако, только одна максимальная повторяющаяся подпоследовательность, а именно x. Вот пример: для x = ABC имеем x2 = ABCABC. Непересекающимися повторяющимися подпоследовательностями здесь являются A, B, C, AB, AC, BC и ABC, каждая из которых является подпоследовательностью максимальной повторяющейся подпоследовательности ABC.
. Имеется, однако, только одна максимальная повторяющаяся подпоследовательность, а именно x. Вот пример: для x = ABC имеем x2 = ABCABC. Непересекающимися повторяющимися подпоследовательностями здесь являются A, B, C, AB, AC, BC и ABC, каждая из которых является подпоследовательностью максимальной повторяющейся подпоследовательности ABC.
Итак, видимо, имеет смысл следующее ограничение: следует искать только максимальные непересекающиеся повторяющиеся подпоследовательности.
Теперь мы можем дать более строгую формулировку задачи. Сначала, однако, введем подходящие обозначения.
Во-первых, строка x длины |x| = m записывается как x1x2...xm, где xi представляет i-й символ x.
Подстрока
xixi+1 … xj строки x, где i j
j m, будет обозначаться x(i,j). В случае, когда i>j, обращенная подстрока обозначается так xR(i,j).
m, будет обозначаться x(i,j). В случае, когда i>j, обращенная подстрока обозначается так xR(i,j).
Обычно x будет обозначать искомый образец, а y – текстовую строку; |x| = m, |y| = m и, конечно, m n.
n.
Пример
x = trismegistus
|x| = 12
x(7,10) = gist
xR(7,4) = gems
A = {
! « # $ % & ` ( ) * + , - . / 0 1 2 3 4 5 6 7 8 9 : ; < = > ? @
A B C D E F G H I J K L M N O P
Q R S T U V W X Y Z [ / ] ^ _ ‘ a b c d e f g h
i j k l m n o p q r s t u v w x y z { | }~
}
 = A
= A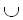 { ‘ ’ }
{ ‘ ’ }
Вариант алфавита #1. Каждый символ является непустой строкой (часто говорят словом) над A. Алфавит символов W является бесконечным, и задается положительным замыканием A:
|
W = A+ |
(2.2) |
Цепочки литер образуют слова (часто говорят предложения), разделителем служит пробел. Множество всех предложений будет обозначаться SW. Оно было бы равно W+, если бы не требование, чтобы все слова разделялись символом, не принадлежащим алфавиту A. На самом деле, SW совпадает с положительным замыканием  .
.
Вариант алфавита #2. Каждый символ входит в  . Алфавит символов, таким образом, равен
. Алфавит символов, таким образом, равен  , последовательность является непустой строкой над
, последовательность является непустой строкой над  . Множество всех последовательностей
. Множество всех последовательностей 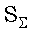 , задается как
, задается как
|
|
(2.3) |
Задача. Для данной последовательности x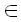 S идентифицировать и локализовать максимальные непересекающиеся повторяющиеся подпоследовательности x.
S идентифицировать и локализовать максимальные непересекающиеся повторяющиеся подпоследовательности x.
К основным обсуждаемым в литературе задачам анализа строк относятся: сопоставление строк, вычисление расстояния между строками, нахождение самой длинной общей подпоследовательности, нечеткое сопоставление строк и поиск самой длинной повторяющейся подстроки. Ниже представлены постановки этих задач и различные подходы к их решению.
Задача сопоставления строк обычно формулируется следующим образом.
Пусть заданы образец x, |x| = m, и текст y, |y| = n, где m, n > 0 и m n. Если x содержится в y, найти позицию первого вхождения x в y, то есть определить наименьшее i, при котором y(i, i+m-1) = x(1,m). В обобщенной задаче требуется локализовать все вхождения x в y. Алгоритмы, решающие основную задачу, как правило, легко распространить на обобщенную.
n. Если x содержится в y, найти позицию первого вхождения x в y, то есть определить наименьшее i, при котором y(i, i+m-1) = x(1,m). В обобщенной задаче требуется локализовать все вхождения x в y. Алгоритмы, решающие основную задачу, как правило, легко распространить на обобщенную.
Довольно полный обзор алгоритмов сопоставления строк, куда вошли и последние статьи Сандея [Sunday (1990)], принадлежит Пирклбауеру [Pirklbauer (1990)]. Кроме того, исчерпывающее сравнение эффективности различных алгоритмов по времени и затратам памяти проведено Гоннетом и Бейза-Ейтсом [Gonnet and Baeza-Yates (1991)]. Не следует также пренебрегать обзорами Ахо [Aho, 1990; 1980] и Седжвика [Sedgewick (1983)].
Наивный подход к этой задаче: продвигаясь по тексту символ за символом, тупо сравнивать x с подстроками строки y. При этом строку входного текста приходится записывать в буфер, так как в случае неудачи сопоставления необходимы возвраты. Для худшего случая наивному алгоритму требуется время O(mn), однако на практике, при работе с обычными текстами, его средняя эффективность равна O(m + n).
По теореме Кука [Cook, 1972] о детерминированных магазинных автоматах существует алгоритм, который решает задачу сопоставления строк в худшем случае за время O(m+n). Как показал Ривест [Rivest, 1977], любой алгоритм сопоставления строк должен проверить в худшем случае не менее n-m+1 символов строки текста. Отсюда следует, что нельзя найти решение задачи сопоставления строк, которое в худшем случае вело бы себя сублинейно по n.
В 1970 году Кнут познакомился с теоремой Кука и вывел из нее алгоритм сопоставления строк. Его алгоритм затем модифицировал Пратт (Pratt) так, что время работы алгоритма перестало зависеть от размера алфавита символов. Полученный в результате алгоритм был в 1969 году без теоремы Кука независимо построен Моррисом (Morris), который хотел избежать перебора с возвратами в текстовом редакторе. Вот краткое описание этого алгоритма [Knuth, Morris, Pratt, 1977].
В его основе лежит идея, состоящая в том, что если полнее использовать информацию, получаемую в процессе поиска, то можно избежать возвратов при несовпадении. Текстовая строка последовательно просматривается слева направо. Если попытка сопоставления потерпела неудачу на символе xj, то предыдущие j-1 символов текста нам известны: они содержатся в x(1,j-1). Этот факт, конечно, желательно использовать, чтобы определить величину шага вправо (смещение) для следующей попытки сопоставления с образцом. Смещения содержатся в дополнительной таблице next, которая перед началом поиска вычисляется по образцу за время O(m).
Наихудший случай для алгоритма – строки Фибоначчи: для них алгоритму требуется время O(m+n). Этот метод хорошо работает для образцов и текстов с большим количеством повторов, что, впрочем, редко встречаются на практике. Поэтому в среднем алгоритм Кнута-Морриса-Пратта не намного быстрее наивного метода. Зато ему не требуется проводить перебор с возвратами во входном тексте, что избавляет от необходимости использовать схемы буферизации, а это полезно, например, при чтении текстов с устройств последовательного доступа.
Пирклбауер [Pirklbauer, 1992] предложил вариант алгоритма Кнута-Морриса-Пратта, в котором сопоставления образца и текста производятся справа налево, как у Бойера и Мура (Boyer, Moore), см. ниже. Средняя эффективность увеличилась, однако анализ входного текста перестал быть строго последовательным.
Гораздо более быстрый метод поиска был открыт в 1974 году Бойером и Муром, и, независимо от них, Госпером (Gosper). Позже была найдена улучшенная версия этого алгоритма (Boyer, Moore, 1977), в которой были учтены предложения Б. Купера (B.Kuiper), Д. Е. Кнута и Р. В. Флойда.
Скорость в алгоритме Бойера-Мура достигается за счет того, что удается пропускать те части текста, которые заведомо не участвуют в успешном сопоставлении. Для большого алфавита и маленького образца среднее число сравнений равно n/m символов, в худшем случае потребуется O(m+n) сравнений. Образец продвигается по тексту слева направо, однако посимвольные сравнения образца и текста от каждой пробной позиции выполняются справа налево. Итак, сначала сравниваем xm и ym. Если ym не содержится в x, то никакая из подстрок y, начинающаяся с одного из следующих m символов, заведомо не может совпасть с x. Поэтому следующей позицией образца может стать m+1 и сравниваться будут xm и y2m. Фактический сдвиг образца определяется большим из значений, взятых из двух заранее вычисленных таблиц. Одна из них, таблица skip, индексируется «отвергающим» символом текста – тем, который вызвал несовпадение (эвристика вхождения), а другая основывается на таблице next алгоритма Кнута-Морриса-Пратта (эвристика совпадения). Предобработка образцов для алгоритма Бойера-Мура, описанная в примечании к работе Кнута, Морриса и Пратта [Knuth, Morris, Pratt, 1977], фактически некорректна, однако она была исправлена Риттером [Rytter, 1980).
Сколько же символов необходимо сравнить, чтобы определить все вхождения образца в текст в худшем случае? Алгоритму Бойера-Мура потратит на это O(n+rm) сравнений, где r – число найденных совпадений. Кнут, Моррис и Пратт (Knuth, Morris, Pratt, 1977) предложили модифицированную версию алгоритма Бойера-Мура, которой требуется не более 6n сравнений в случае, когда образец ни разу не появляется в тексте. Губас и Одлыжко [Guibas, Odlyzko, 1977] улучшили этот показатель до 4n и выдвинули гипотезу, что граница равна 2n. Галил [Galil, 1979] также предложил вариант этого алгоритма, который был улучшен Апостолико и Джанкарло [Apostolico, Giancarlo, 1986]. Их версия требует не больше 2n сравнений символов, независимо от количества появлений образца в тексте. Это сделано ценой всего лишь очень небольшого увеличения расходов на предварительную обработку образца, которые по-прежнему остаются линейными по m. В среднем, однако, эти методы не дают значимого улучшения.
Хорспул [Horspool, 1980] показал, что упрощенная форма алгоритма Бойера-Мура с только одной таблицей, индексируемой отвергающими символами текста, по производительности сравнима с исходной. На самом деле, как установлено в работе Бейза-Ейтса [Baeza-Yates, 1989a] на основании аналитических и эмпирических исследований известных алгоритмов, метод Бойера-Мура-Хорспула является наилучшим с точки зрения эффективности в среднем случае почти для всех длин образца и мощностей алфавита.
Бейза-Ейтс [Baeza-Yates, 1989b] сравнил алгоритмы Бойера-Мура-Хорспула, Кнута-Морриса-Пратта и наивный подход по средней эффективности. Рассматривалась задача отыскания всех вхождений образца, а образцом и текстом служили случайные строки (то есть последовательности символов, независимо и с одинаковой вероятностью выбираемые из алфавита). Эмпирически были получены довольно узкие границы для ожидаемого числа сравнений символов в этих методах поиска. Предложен смешанный алгоритм, комбинирующий подходы Бойера-Мура и Кнута-Морриса-Пратта. Оказалось, что при поиске в английском тексте эффективность смешанного алгоритма слегка выше, чем у метода Бойера-Мура-Хорспула.
Среднее время работы алгоритма Бойера-Мура уменьшается с увеличением алфавитов или длин шаблонов. Увеличения эффективности можно, таким образом, достичь путем увеличения алфавита. Эта идея обсуждалась Кнутом, Моррисом и Праттом [Knuth, Morris, Pratt,1977] и Шабаком [Schaback, 1988]. Бейза-Ейтс [Baeza-Yates, 1989a] предложил простое преобразование алфавита, ведущее к практичной реализации варианта Бойера-Мура-Хорспула. Если k символов шаблона объединить в суперсимвол, размер шаблона сократится с |x| до m-k+1 и одновременно размер алфавита увеличится до  k, где
k, где  – исходный алфавит. Было показано, что этот подход представляет практический интерес, когда алфавит мал или шаблон велик, и сообщалось об экспериментах, в которых увеличение скорости достигало 50% (например, для k = 2,
– исходный алфавит. Было показано, что этот подход представляет практический интерес, когда алфавит мал или шаблон велик, и сообщалось об экспериментах, в которых увеличение скорости достигало 50% (например, для k = 2,  = 8 и случайного текста).
= 8 и случайного текста).
Бейза-Ейтс [Baeza-Yates, 1989a] выдвинул также предложение, позволяющее увеличить эффективность поиска в неравномерно распределенном тексте, например, в английском. Он рассматривал оптимальное упорядочивание сравнений символов, основанное на их вероятностном распределении в тексте. Это достигается либо путем предварительной обработки текста, либо использованием априорной информации об источнике текста. Например, более редкие символы можно сравнивать до более частых, что позволяет раньше выявлять несовпадение.
Для адресации в таблице эвристики вхождения, применяемой в алгоритме Бойера-Мура, Сандей [Sunday, 1990] предложил использовать символ, находящийся в тексте непосредственно за отвергающим. Он разработал три варианта, которые отличаются друг от друга порядком сравнения символов образца и текущей подстроки текста. В алгоритме Быстрый поиск (Quick Search) сравнения производятся слева направо. Алгоритм Максимальный сдвиг (Maximal shift) упорядочивает сравнения так, чтобы расстояние до следующей позиции образца в случае несовпадения было максимальным. И, наконец, в алгоритме Оптимальное несовпадение (Optimal mismatch) используется идея Бейза-Ейтса, которая, как говорилось выше, состоит в том, чтобы более редкие символы сравнивать раньше частых. Смит [Smith, 1991] разработал адаптированную версию метода Оптимальное несовпадение Сандея, обладающую тем преимуществом, что она не требует предварительной информации о тексте.
Хьюм и Сандей [Hume, Sunday,1991] выделили обобщенную структуру оптимизированных реализаций метода Бойера и Мура (1977), включающую быстрый цикл пропусков, и исследовали семейство алгоритмов, основанных на ней. Были разработаны два новых варианта, соответствующих этой структуре: Улучшенный алгоритм Бойера-Мура (Tuned Boyer-Moore) и алгоритм Наименьшая цена (Least Cost).
Другой подход к задаче сравнения строк состоит в использовании хеширования. Этот метод, позволяет проверить, входит ли образец в строку текста, но не сообщает, где именно; метод был предложен Харрисоном [Harrison, 1971]. Этот метод основан на сравнении сигнатур строк и требует предварительной обработки текста. Поэтому его можно применять, например, для просмотра больших редко меняющихся текстовых файлов.
Карп и Рабин [Karp, Rabin, 1987] также предложили алгоритм с хешированием, но не требующий предобработки просматриваемого текста. Их метод похож на наивный подход, однако они предлагают сравнивать в последовательных позициях текста не m-символьные строки, а их сигнатуры. Таким образом, задача сравнения двух строк сводится к более простой задаче сравнения двух целых чисел. Используется хеш-функция, которая позволяет вычислять сигнатуры подстрок текста рекурсивно. Этот алгоритм сопоставления строк можно применять для сравнения многомерных шаблонов, например, в приложениях по обработке изображений. В худшем случае, который весьма маловероятен, алгоритму требуется время O(mn), однако его средняя эффективность равна O(m+n).
Относительная эффективность описанных выше алгоритмов изучалась многими исследователями как теоретически, так и эмпирически; см., например, Хорспул [Horspool, 1980], Смит [Smith, 1982], Байес-Ейтс [Baeza-Yates, 1989a], Девис и Боушер [Davis, Bowsher, 1986], Пирклбауер [Pirklbauer, 1992]. Они сходятся на том, что в общем случае лучшим является алгоритм Бойера-Мура-Хорспула. Как указывалось ранее, Бейза-Ейтс [Baeza-Yates, 1989a] дает эту рекомендацию практически для всех длин образцов и мощностей алфавита. В экстремальных случаях, когда образцы очень малы (m = 1…3), а их длины сравнимы с длинами текстов (то есть, m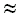 n), лучше использовать наивный подход. Хорспул обнаружил, что средняя эффективность его упрощенного варианта и исходной версии алгоритма Бойера-Мура примерно одинаковы, причем оба алгоритма лучше, чем наивный подход, реализуемый с помощью специальных машинных инструкций для символьного поиска, когда m
n), лучше использовать наивный подход. Хорспул обнаружил, что средняя эффективность его упрощенного варианта и исходной версии алгоритма Бойера-Мура примерно одинаковы, причем оба алгоритма лучше, чем наивный подход, реализуемый с помощью специальных машинных инструкций для символьного поиска, когда m 6.
6.
Несмотря на теоретическую элегантность, алгоритм Кнута-Морриса-Пратта, не допускающий перебора с возвратами, не дает на практике значительного преимущества в скорости по сравнению с методом грубой силы. Он, однако, может быть хорош, когда 
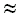 n [Baeza-Yates, 1989a], или в случае бинарных строк, то есть когда
n [Baeza-Yates, 1989a], или в случае бинарных строк, то есть когда  = 2 [Davies, Bowsher, 1986). Подход Бойера-Мура, несмотря на то, что символы могут проверяться более одного раза и допускаются возвраты, в целом оказывается значительно более эффективным.
= 2 [Davies, Bowsher, 1986). Подход Бойера-Мура, несмотря на то, что символы могут проверяться более одного раза и допускаются возвраты, в целом оказывается значительно более эффективным.
По быстродействию метод Карпа-Рабина, основанный на хешировании, сильно уступает остальным, зато его можно обобщить на многомерные задачи и применять, скажем, в приложениях, связанных с обработкой изображений.
Что касается изменений, внесенных Сандеем в подход Бойера-Мура, Пирклбауер [Pirklbauer, 1992) рекомендует объединить Быстрый поиск Сандея с упрощенным вариантом Бойера-Мура. Однако, он не советует использовать алгоритмы Максимальный сдвиг и Оптимальное несовпадение из-за чрезмерной длины кода и большого объема предварительных вычислений, что особенно значимо, если надо найти только первое появление образца. Хьюм и Сандей [Hume, Sunday, 1991] сообщают о значительно большей эффективности их новых методов по сравнению с исходным алгоритмом Бойера-Мура. Однако, при этом они также не учитывают груз предварительных вычислений.
Несмотря на высокую производительность подхода Бойера-Мура, его внедрение в практику до некоторой степени затруднено сложностью алгоритма предварительной обработки, в частности, эвристики совпадения. Хорспул [Hoorspool, 1980] пишет: «многие программисты не верят, что алгоритм Бойера и Мура (если они о нем слышали) оказывается действительно практичным». Седжвик [Sedgewick, 1983] также замечает: «и алгоритм Кнута-Морриса-Пратта, и алгоритм Бойера-Мура требуют алгоритмически сложных предобработок образца, которые трудно понять и которые ограничивают их использование». В самом деле, Моррис обнаружил, что, по прошествии нескольких месяцев, его первоначальная реализация поиска в текстовом редакторе оказалась искаженной разнообразными ненужными исправлениями, поскольку была слишком сложной для других программистов, которые не понимали ее [Knuth, Morris, Pratt, 1977]. Хьюм и Сандей [Hume, Sunday, 1991] добавляют: «из-за того, в частности, что лучшие алгоритмы, представленные в литературе, трудны для понимания и реализации, быстрые и практичные алгоритмы не стали еще общеизвестными». Борясь за более последовательный подход к развитию алгоритмов, и против «широко распространенной хаотической реализации алгоритмов», Вуд [Woude, 1989] заявляет, что предобработка в алгоритме Кнута-Морриса-Пратта должна быть не более трудной для понимания, чем сама процедура поиска. Позже были предприняты некоторые попытки популяризации подхода Бойера-Мура, особенно его упрощенной формы; см., например, Менико [Menico, 1989]. Для разъяснения этой области Хьюм и Сандей [Hume, Sunday, 1991] представили классификацию различных алгоритмов, основанных на подходах Кнута-Морриса-Пратта и Бойера-Мура.
Понятие функции, измеряющей расстояние, или метрики, используется в самых разных областях и часто используется для оценки сходства двух векторов. Такие функции применяют для определения силы связи двух признаков, или, например, в распознавании образов при сопоставлении шаблонов с различными частями изображений. Как известно, метрика задается функцией d с следующими свойствами:
| Неотрицательность |
d(x,y) 0 0 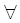 x,y x,y |
(3.1) |
| Свойство нуля |
d(x,y) = 0 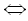 x = y x = y |
(3.2) |
| Симметричность |
d(x,y) = d(y,x) 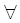 x,y x,y |
(3.3) |
| Неравенство треугольника |
d(x,z) d(x,y) + d(y,z) d(x,y) + d(y,z) 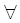 x,y,z x,y,z |
(3.4) |
Последовательности длины n иногда объявляют векторами в Rn и применяют обычные расстояния: "шахматной доски" maxi |xi-yi|, "сити-блок" ("городских кварталов") 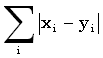 и Евклида
и Евклида 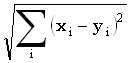 .
.
При обработке строк, однако, символы не всегда уместно считать числами, несмотря на то, что коды символов являются ими. Кроме того, часто требуется сравнивать строки разной длины. Поэтому для сравнения строк обычно используют метрики, оценивающие максимальную стоимость преобразования одной строки в другую. В общем случае, операциям редактирования, используемым в этом преобразовании, а именно замене символов, их вставке и удалению, можно назначить разные цены. Последние две операции иногда объединяют в одну и называют вставуд (indel; от insertion и deletion).
Расстояние Хемминга [Hamming, 1982] между двумя строками одинаковой длины определяется как число позиций, в которых символы не совпадают. Это эквивалентно минимальной цене преобразования первой строки во вторую в случае, когда разрешена только операция замены с единичным весом. Если допускается сравнение строк разной длины, то, как правило, требуются также вставка и удаление. Если придать им тот же вес, что и замене, минимальная общая цена преобразования будет равна одной из метрик, предложенных Левенштейном [Levenstein, 1965]. Другая метрика равна минимальной цене преобразования в случае, когда разрешены только вставка и удаление. Это эквивалентно назначению цены 1 удалению и вставке, и 2 замене, так как последнюю можно заменить парой вставка-удаление. Первую из этих метрик мы ниже называем расстоянием Левенштейна, а вторую – расстоянием редактирования.
Такие метрики применяются в качестве мер сходства в самых разных областях, например, для оценки степени гомологичности генетических последовательностей. Заметим, однако, что не все функции, измеряющие расстояние между строками, являются метриками. Например, если цены операций редактирования являются функциями конкретных символов, неравенство треугольника может не выполняться. Информацию о множестве областей – от молекулярной биологии до обработки речи, – в которых применяются функции расстояния, можно найти у Санкофа и Краскела [Sankoff, Kruskall, 1983].
Оставшаяся часть раздела представляет собой обзор основных алгоритмов вычисления расстояний между строками (иногда в качестве приложения имеют в виду поиск различий в файлах или задачу построчного сравнения), а также родственную проблему нахождения самой длинной общей подпоследовательности. Последний обзор этих задач можно найти в работе Ахо [Aho, 1990], а обзор сложности результатов для задач об общей подпоследовальности представлен Хиршбергом [Hirschberg, 1983]. Более подробное исследование основных алгоритмов отложено до следующей главы. Однако, прежде чем идти дальше, следует дать формулировку задачи.
Задача о расстоянии между строками
Для данных строк x и y, где |x|, |y| > 0, и метрики d, задающей расстояния между строками, вычислить d(x,y).
В задаче поиска различий между файлами x и y через xi обозначим i-ю строку x, а через yj – j-ю строку y. В этом случае требуется определить минимальную последовательность операций редактирования, преобразующую x в y.
Задача о наибольшей общей подпоследовательности
Напомню, что подпоследовательность строки получается путем исключения из нее нуля или более символов, не обязательно смежных. Общая подпоследовательность двух строк – это строка, являющаяся подпоследовательностью каждой из них. Самая длинная из таких строк называется, понятное дело, самой длинной общей подпоследовательностью.
Итак, задача состоит в том, чтобы для данных строк x и y (|x|, |y| > 0) найти |lcs(x,y)|, где lcs(x,y) – самая длинная общая подпоследовательность (longest common subsequence) x и y. Как правило, требуется найти не только длину lcs(x,y), но и саму эту последовательность.
Метод вычисления расстояния между двумя строками, основанный на методе динамического программирования [Bellman, Dreyfus, 1962], был открыт независимо несколькими исследователями. Санкоф и Краскел [Kruskal, 1983] приписывают процедуры, основанные на этом принципе, следующим авторам: Винтсюк [Vintsyuk, 1968]; Нидлман и Вунч [Needleman, Wunch, 1970]; Величко и Загоруйко [Velichko, Zagoruyko, 1970]; Сако и Чиба [Sakoe, Chiba, 1970; 1971]; Санкоф [Sankoff, 1972]; Райчер, Коен и Вонг [Reichert, Cohen, Wong, 1973]; Хатон [Haton, 1973]; Вагнер и Фишер [Wagner, Fisher, 1974]; Хиршберг [Hirschberg, 1975].
Идея метода динамического программирования состоит в том, чтобы последовательно оценивать расстояния между все более длинными префиксами строк – до получения окончательного результата. Промежуточные результаты вычисляются итеративно и хранятся в массиве длины (m+1) (n+1), что приводит к времени и памяти O(mn). Метод Вагнера и Фишера [Wagner, Fisher, 1974], основанный на структуре, которую они назвали следом (trace), позволяет вычислить lcs прямо по заполненному массиву расстояний.
(n+1), что приводит к времени и памяти O(mn). Метод Вагнера и Фишера [Wagner, Fisher, 1974], основанный на структуре, которую они назвали следом (trace), позволяет вычислить lcs прямо по заполненному массиву расстояний.
Хиршберг [Hirschberg, 1975] модифицировал метод Вагнера и Фишера так, что временные затраты остались равными O(mn), но затраты памяти стали линейными, не квадратичными. В его методе итеративно вычисляются длины lcs последовательно увеличивающихся префиксов строк, а не расстояния между ними. Экономия памяти происходит за счет того, что в каждый заданный момент времени в памяти хранятся только две строки массива, требуемого динамическому программированию. Потеря остальной части массива, однако, приводит к более сложному методу выделения lcs двух строк. Предлагается рекурсивно делить пополам первую строку и получать две lcs – для каждой половины и подходящей подстроки второй строки. Рекурсия раскручивается до тех пор, пока, в конце концов, выделение lcs не станет тривиальным. Окончательная lcs полных строк после этого получается простой конкатенацией кусков строк, полученных во время рекурсии.
Хант и Мак-Илрой [Hunt, McIlroy, 1976] применили алгоритм Хиршберга для реализации команды diff Юникса. Он хорошо работает на коротких файлах, однако квадратичная временная сложность приводит к значительному уменьшению скорости выполнения по мере увеличения входных файлов. Однако, позже Мак-Илрой добился значительного улучшения программы, применив алгоритм поиска lcs, разработанный Хантом и Шиманским [Hunt, Szymanski, 1977].
Подход Ханта и Шиманского к выделению lcs двух строк эквивалентен определению самого длинного монотонно возрастающего пути на графе, составленном из узлов (i,j), таких, что xi = yi. В то время как описанным методам всегда требуется квадратичное время, время этого алгоритма для строк одинаковой длины – всего лишь O((r+n) log(n)), где r – общее число упорядоченных пар позиций, в которых символы двух строк совпадают. В худшем случае может понадобиться сравнивать каждый элемент x с каждым символом y, что приводит к n2 таких упорядоченных пар и сложности O(n2
log(n)), где r – общее число упорядоченных пар позиций, в которых символы двух строк совпадают. В худшем случае может понадобиться сравнивать каждый элемент x с каждым символом y, что приводит к n2 таких упорядоченных пар и сложности O(n2 log(n)). Однако, во многих приложениях, например, в задаче поиска различий в файлах, где каждую строку файла естественно считать атомом, можно ожидать, что r будет близко к n, а это дает эффективность O(n
log(n)). Однако, во многих приложениях, например, в задаче поиска различий в файлах, где каждую строку файла естественно считать атомом, можно ожидать, что r будет близко к n, а это дает эффективность O(n log(n)) – существенное улучшение по сравнению с процедурами, требующими квадратичного времени.
log(n)) – существенное улучшение по сравнению с процедурами, требующими квадратичного времени.
Машек и Патерсон [Masek, Paterson, 1980; 1983] разработали алгоритм поиска расстояния между строками, основанный на методе динамического программирования Вагнера и Фишера, временная сложность которого субквадратична даже в худшем случае. Этому методу, однако, требуется, чтобы алфавит был конечным, а ценовые веса – целыми множителями фиксированного действительного числа. Алгоритм использует метод «четырех русских» [Арлазаров, Диниц, Кронрод и Фараджев, 1970], его время в худшем случае равно O(n2/log n) – для строк равной длины. Основная идея этого метода состоит в разбиении матрицы расстояний на совокупность подматриц. Их нижние и правые края можно затем вычислить по аналогичным краям подматриц, примыкающих к текущей сверху и слева, и соответствующим подстрокам x и y, с помощью предварительно вычисленной таблицы. Хотя асимптотически этот алгоритм быстрее обычного динамического программирования, Машек и Патерсон [Masek, Patterson, 1983) указывают, что его следует использовать только для длинных строк; например, при вычислении расстояния редактирования между двумя бинарными строками он становится по-настоящему быстрым, только когда длины строк превосходят 262418.
Шиманский показал, что для алфавитов неограниченной длины можно приспособить алгоритм Машека и Патерсона, получив время O(n2 (log log n)2 / log n), что все еще субквадратично асимптотически[Hirschberg, 1983].
Совсем другой подход, особенно хорошо работающий, когда строки схожи, был предложен независимо Укконеном [Ukkonen, 1983, 1985a] и Майерсом [Myers, 1986]. В основе их методов лежит поиск пути минимальной цены на графе, который составлен из вершин матрицы расстояний, а также горизонтальных, вертикальных и диагональных ребер, соответствующих связям между смежными узлами. Требуемый путь начинается в (0, 0) и заканчивается в (m, n).
При методе Укконена ненужных вычислений в матрице расстояний удается избежать за счет сравнения с порогом расстояния между строками. Процесс повторяется для последовательно возрастающих пороговых значений, пока не превзойдет это расстояние, что и дает требуемое расстояние, причем на это тратится время O(md). Фактическое расстояние редактирования можно затем восстановить по вычисленным значениям матрицы расстояний – как в алгоритме Вагнера-Фишера.
Подход Майерса (Myers) состоит в том, чтобы находить конечные точки все более длинных путей в графе, пока не будет достигнута точка (m, n). В худшем случае на это потребуется время O((m+n)d), однако Майерс показал, что в среднем временная сложность равна O(m+n+d2). Кроме того, были разработаны версия алгоритма с линейной памятью и вариант, который в худшем случае дает время O((m+n)log(m+n)+d2). Последний основан на применении суффиксных деревьев Мак-Крейта [McCreight, 1976] и его асимптотическое поведение представляет теоретический интерес. Он, однако, нежизнеспособен из-за сложности используемых в нем алгоритмов.
Апостолико и Гиерра [Apostolico, Guerra, 1987] проанализировали методы поиска самой длинной общей подпоследовательности Хиршберга и Ханта-Шиманского и изобрели родственные алгоритмы, содержащие некоторые улучшения. Для случая m << n их версия алгоритма Хиршберга быстрее исходной, так как их версия имеет временную сложность O(m2 min{log
min{log , log m, log(2n/m)}), где
, log m, log(2n/m)}), где  – алфавит. Как указывалось выше, в худшем случае эффективность алгоритма Ханта и Шиманского хуже квадратичной. Однако, Апостолико и Гиерра удалось ограничить его поведение в худшем случае до квадратичного. Фактической временной границей их версии алгоритма является O(m
– алфавит. Как указывалось выше, в худшем случае эффективность алгоритма Ханта и Шиманского хуже квадратичной. Однако, Апостолико и Гиерра удалось ограничить его поведение в худшем случае до квадратичного. Фактической временной границей их версии алгоритма является O(m log(n) + t
log(n) + t log(2mn/t)), где t
log(2mn/t)), где t r – это число доминантных совпадений между двумя сравниваемыми строками.
r – это число доминантных совпадений между двумя сравниваемыми строками.
Исследованию сложности задачи lcs для частных моделей вычислений посвящено много работ. Вонг и Чандра [Wong, Chandra, 1976] вывели границы для вычисления расстояний между строками в терминах функции цен редактирования, когда при сравнении символов ограничиваются проверкой равенства. Они показали также, что при этих ограничениях для нахождения lcs требуется O(mn) сравнений символов.
Используя вычислительную модель дерева решений ‘равно-неравно’, Ахо, Хиршберг и Ульман [Aho, Hirschberg, Ullman, 1976] вывели границы задачи lcs в терминах объема алфавита символов. Они обнаружили, что в худшем случае всегда требуется минимум O(n2) сравнений для строк равной длины, и O(n
 ) для n
) для n
 , где
, где  – алфавит.
– алфавит.
Для случая, когда используется лексикографическое упорядочение символов, позволяющее сравнивать их по величине, Хиршберг [Hirschberg, 1978] показал, что минимальное требуемое число сравнений равно O(n log n).
log n).
Подводя итоги сравнения эффективности разных подходов к задачам, связанным с поиском расстояний между строками и проблеме поиска lcs, можно сказать следующее. Метод динамического программирования Вагнера и Фишера прост в реализации, однако требует квадратичных затрат времени и памяти. Поэтому для больших приложений предпочтительна версия Хиршберга с линейным временем. Однако, алгоритм Ханта-Шиманского во многих приложениях имеет значительно более высокую эффективность, которая достигается ценой того, что в худшем случае временная сложность становится больше квадратичной. Алгоритм Машека и Патерсона – единственный из известных алгоритмов, которому в худшем случае требуется субквадратичное время. Однако дополнительные вычислительные издержки этого метода приводят к тому, что он становится эффективнее прямого метода динамического программирования только для очень длинных срок. В случае, когда две сравниваемые строки похожи, то есть когда d мало, хороши методы Укконена или Майерса.
Схожие проблемы часто возникают в молекулярной биологии, где требуется определить, какие части последовательностей похожи, или гомологичны. См., например, обсуждение в работе Санкофа и Краскела [Sankoff, Kruskal, 1983], которые расширили метод нахождения локальных наложений Смита и Вотермана [Smith, Waterman, 1981]. Помимо минимизации расстояния между частями последовательностей, требуются также некоторые средства для максимизации их длин, так как всегда найдутся тривиальные части последовательностей, расстояние между которыми будет нулевым. Поэтому используется вариант метода динамического программирования, в котором совпадения поощряются, а замены, вставки и удаления штрафуются. Это достигается назначением положительного веса совпадениям, и отрицательных весов операциям редактирования. Однако квадратичная природа метода динамического программирования делает его непрактичным для применения в очень больших базах последовательностей. Поэтому для решения этой задачи были разработаны различные эвристические методы, в частности метод Липмана и Пирсона [Lipman, Pearson, 1985] и Альтшуля и др. [Altschul et al., 1990].
Кроме того, изучалась задача вычисления расстояния между двумя строками в случае, когда помимо вставки, удаления и замены в качестве операции редактирования разрешена перестановка смежных символов. Этот вариант позволяет, например, при вычислении расстояния учитывать ошибки, возникающие при вводе текста с клавиатуры. Несмотря на значительное увеличение сложности при анализе такой ситуации, задача по-прежнему разрешима за квадратичное время методом динамического программирования; см. Лоуренс и Вагнер [Lowrance, Wagner, 1975], Вагнер [Wagner, 1975, 1983].
Обобщением задачи lcs является задача N-lcs, в которой требуется определить самую длинную общую подпоследовательность для множества из N строк. Если то, что x является подпоследовательностью y, записывать как x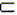 y, задачу можно сформулировать следующим образом. Для заданного множества X = {x1, x2,…, xN} из N строк найти последовательность N-lcs(X) максимальной длины, такую, что N-lcs(X)
y, задачу можно сформулировать следующим образом. Для заданного множества X = {x1, x2,…, xN} из N строк найти последовательность N-lcs(X) максимальной длины, такую, что N-lcs(X)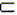 xi для всех i
xi для всех i![]() [1, N]. В этих обозначениях упоминавшаяся выше задача lcs, является задачей 2-lcs.
[1, N]. В этих обозначениях упоминавшаяся выше задача lcs, является задачей 2-lcs.
Майер [Maier, 1978] показал, что для алфавитов размера два и более задача определения |N-lcs| является NP-полной при любых N; см. тж. Карп [Karp, 1972]. Отсюда следует, что нет смысла применять поиск N-lcs(X) в таких, например, задачах, как сжатие данных, поскольку полученные решения неизбежно окажутся неприменимыми (по крайней мере до тех пор, пока не будут найдены полиномиальные подходы к решению NP-полных задач). Например, применение динамического программирования к задаче N-lcs потребует для строк длины n времени и памяти O(nN).
Для случаев, когда при решении задачи N-lcs для строк длины n величину N можно считать константой, Бейза-Ейтс [Baeza-Yates, 1991] предложил метод, которому в худшем случае по-прежнему требуются время и память порядка O(nN), но, который, однако, в среднем ведет себя лучше. Его подход состоит в построении частично детерминированного конечного автомата, известного как направленный ациклический граф подпоследовательностей (Directed Acyclic Subsequence Graph, DASG), который способен распознавать все последовательности строк множества X. При построении графа его ребра помечаются числом строк, разделяющих этот переход. После этого lcs множества X можно найти, находя в графе максимальные последовательности ребер с меткой N.
Направленный ациклический граф последовательностей можно построить за время O(N

 n
n log(n)), для этого потребуется память O((N+
log(n)), для этого потребуется память O((N+ )
) n). Обозначим через r количество совпадающих позиций между N строками, в худшем случае оно равно nN, однако в среднем мало по сравнению с этой величиной. Пройти граф можно за время O(r), чтобы получить lcs для совокупности строк потребуется максимум O(r) памяти. Таким образом, затраты времени и памяти у этой процедуры равны соответственно O(r+N
n). Обозначим через r количество совпадающих позиций между N строками, в худшем случае оно равно nN, однако в среднем мало по сравнению с этой величиной. Пройти граф можно за время O(r), чтобы получить lcs для совокупности строк потребуется максимум O(r) памяти. Таким образом, затраты времени и памяти у этой процедуры равны соответственно O(r+N

 n
n log n) и O(r+(N+
log n) и O(r+(N+ )
) n). Эта временная граница лучше, чем у метода Чу и Ду [Hsu, Du, 1984], имеющего аналогичную сложность.
n). Эта временная граница лучше, чем у метода Чу и Ду [Hsu, Du, 1984], имеющего аналогичную сложность.
Майер [Maier, 1978] рассмотрел также задачу N-scs (shortest common supersequence). Это задача нахождения самой короткой общей надпоследовательности для множества из N строк. Строка y называется надпоследовательностью x, если x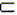 y. Задачу N-scs можно сформулировать следующим образом. Для данного множества X = {x1, x2,… , xN} из N строк найти N-scs(X), последовательность минимальной длины, такую что N-scs(X)
y. Задачу N-scs можно сформулировать следующим образом. Для данного множества X = {x1, x2,… , xN} из N строк найти N-scs(X), последовательность минимальной длины, такую что N-scs(X) xi для всех целых i
xi для всех целых i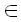 [1,N]. Майер обнаружил, что для алфавита размера
[1,N]. Майер обнаружил, что для алфавита размера  5 задача отыскания N-scs оказывается NP-полной, и высказал предположение, что это верно и для алфавитов мощности
5 задача отыскания N-scs оказывается NP-полной, и высказал предположение, что это верно и для алфавитов мощности  3.
3.
Задачу нахождения самой тяжелой общей подпоследовательности (heaviest common subsequence, hcs) двух строк исследовали Джекобсон и Во [Jacobson, Vo, 1992]. hcs(x,y) – это последовательность, общая для x и y, имеющая при данной весовой функции максимальную сумму весов компонент. В общем случае, функция может зависеть как от самих символов, так и от их положения в исходных строках.
Поиск hcs находит применение, например, при обновлении информации на дисплее. Вставки и удаления в строках, требуемые для преобразования одного экрана в другой, можно вывести по их lcs. Однако для минимизации разрыва вывода предпочтительно первенство отдавать близким парам сопоставленных линий. Поэтому для получения hcs можно использовать весовую функцию минимальных расстояний, которая будет уменьшаться по мере увеличения расстояния между позициями в соответствующих последовательностях сопоставляемых символов. hcs можно находить с помощью адаптированной версии алгоритма динамического программирования lcs, который использовался, например, в библиотеке обновления экранов curses в System V Unix [Vo, 1986].
Джекобсон и Во [Jacobson, Vo, 1992] представили алгоритм hcs, выведенный из алгоритма для вычисления самой тяжелой возрастающей подпоследовательности (his, heaviest increasing subsequence). Он, в свою очередь, был выведен из метода вычисления самой длинной возрастающей подпоследовательности Робинсона-Шенстеда [Schensted, 1961]. Самая длинная возрастающая подпоследовательность – это максимальная подпоследовательность строк, компоненты которой, при заданном линейном упорядочении алфавита, строго возрастают, а самая тяжелая возрастающая подпоследовательность – это возрастающая подпоследовательность с максимальным весом. Этот алгоритм является обобщением метода Ханта-Шиманского и имеет ту же временную сложность. Для весовых функций, не зависящих от положения символов, специальная форма процедуры hcs становится обобщением алгоритма lcs Апостолико-Гиерра.
Обобщенная задача сопоставления строк, включающая в себя нахождение подстрок строки текста, близких к заданному образцу строки, называется также задачей нечеткого сопоставления строк. Эта задача важна для случая, когда в рассмотрение принимаются ошибки, и применяется, например, в молекулярной биологии (обсуждение некоторых приложений можно найти у Ландау, Вишкина и Нуссинова [Landau, Vishlin, Nussinov, 1985]). Задачу нечеткого сопоставления строк можно сформулировать следующим образом:
 n. Пусть даны также целое k
n. Пусть даны также целое k 0 и функция расстояния d. Требуется найти все подстроки s текста y такие, что d(x, s)
0 и функция расстояния d. Требуется найти все подстроки s текста y такие, что d(x, s) k.
k.Задача, таким образом, состоит в том, чтобы при заданной функции расстояния найти все подстроки текста, отстоящие от образца не более, чем на k. Если d является расстоянием Хемминга, задача называется сопоставлением строк с k несовпадениями, если же d – расстояние Левенштейна, задача называется сопоставлением строк с k различиями (или, иногда, ошибками).
Исчерпывающий обзор алгоритмов нечеткого сопоставления строк представлен в работе Галила и Джанкарло [Galil, Giancarlo, 1988], сравнение сложности некоторых алгоритмов проведено также Гоннетом и Бейза-Ейтсом [Gonnet, Baeza-Yates, 1991].
Наивный подход к задаче сопоставления строк, требующий времени O(mn), легко адаптировать к задаче k несовпадений, разрешив k несовпадений при сравнениях символов подстроки в тексте. Однако, как и для задачи сопоставления строк, для задач k несовпадений и k различий были изобретены более эффективные подходы.
Ландау и Вишкин [Landau, Vishkin, 1985, 1986a] разработали алгоритм для решения задачи k несовпадений, выполняющийся за время O(k(m log(m)+n)). Их подход схож с методом сопоставления строк Кнута-Морриса-Пратта тем, что при проверке строки слева направо используется таблица, вычисляемая на этапе предварительного анализа образца, а информация, получаемая во время поиска, применяется для сокращения числа необходимых сравнений символов.
log(m)+n)). Их подход схож с методом сопоставления строк Кнута-Морриса-Пратта тем, что при проверке строки слева направо используется таблица, вычисляемая на этапе предварительного анализа образца, а информация, получаемая во время поиска, применяется для сокращения числа необходимых сравнений символов.
Ландау и Вишкин [Landau, Vishkin, 1985, 1986a] заметили также, что алгоритм Иванова [Ivanov, 1984] для задачи k несовпадений, имеющий временную сложность O(f(k)(m+n)), быстрее их собственного в случае очень малых k и сравнимых значений m и n. Однако, как они подчеркивают, функция f трудна для понимания, и ограничена снизу 2k. За исключением вышеуказанного случая, их алгоритм быстрее алгоритма Иванова, и к тому же намного проще – они утверждают, что для описания алгоритма Иванова требуется более сорока журнальных страниц.
Версия алгоритма Ландау и Вишкина для задачи k несовпадений с улучшенной предварительной обработкой шаблона была разработана Галилом и Джанкарло (Galil, Giancarlo, 1986, 1988). Временная сложность их версии алгоритма равна O(m log(m)+kn).
log(m)+kn).
Селлерс [Sellers, 1980] показал, как можно приспособить метод вычисления расстояния между двумя строками для решения задачи k различий. После того, как массив расстояний вычислен, можно утверждать, что если в последней строке есть значение, скажем, dm,j, такое, что dm,j k, то существует подстрока, такая, что d(x,s)
k, то существует подстрока, такая, что d(x,s) k. Верно и обратное, если такая подстрока существует, то и соответствующий элемент dm,j обязательно найдется. Подстрока может быть восстановлена обратным проходом по графу зависимостей. Этому методу требуется время O(mn).
k. Верно и обратное, если такая подстрока существует, то и соответствующий элемент dm,j обязательно найдется. Подстрока может быть восстановлена обратным проходом по графу зависимостей. Этому методу требуется время O(mn).
Алгоритм решения задачи k различий, предложенный Укконеном [Ukkonen, 1985b], содержит две стадии – предварительную обработку и собственно анализ текста. На первой стадии строится детерминированный конечный автомат, который затем используется на второй стадии для сканирования входного текста за время O(n). Однако обычно этот алгоритм оказывается непрактичным из-за степенных требований к времени и памяти для предварительной обработки. (Для алфавита  анализ образца потребует затрат времени O(m
анализ образца потребует затрат времени O(m

 min{3m,2k|
min{3m,2k| |kmk+1}) и памяти O((
|kmk+1}) и памяти O(( +m)
+m) min{3m,2k
min{3m,2k kmk+1}).
kmk+1}).
Ландау и Вишкин разработали несколько алгоритмов k различий, основанных на эффективном, с временем O(md), методе вычисления межстроковых расстояний Укконена [Ukkonen, 1983, 1985a]. Предварительный анализ образца в этих алгоритмах позволяет использовать известную информацию при последующей обработке текста. Их алгоритм [Landau, Vishkin, 1985] последовательно проверяет текст на вхождение образца – допуская до k различий. Алгоритм выполняется за время O(m2+k2n) и требует памяти O(m2). Эффективность этого метода позже [Landau, Vishkin, 1988] была улучшена, так что он стал требовать O(m) памяти и O(k2n) времени для алфавитов фиксированной величины и O(m log(m)+k2n) для неограниченных алфавитов. Улучшенная предобработка образца в этом методе позволяет использовать суффиксное дерево (построенное с использованием алгоритма Вейнера [Weiner, 1973]), а стадия анализа текста включает нахождение в нем ближайшего общего предка (lowest common ancestor, LCA); Харел и Тарьян [Harel, Tarjan, 1984], Шибер и Вишкин [Schiber, Vishkin, 1988]. Ландау и Вишкин [1986b, 1989] изобрели также другой алгоритм k различий, включающий использование суффиксного дерева. Алгоритм начинает с очень эффективного вычисления матрицы расстояний между строками, после чего отслеживает позиции текста, в которых заканчиваются подстроки, совпадающие с образцом с точностью до k различий. Их методу требуется время O(kn) для алфавитов фиксированной величины и O(n
log(m)+k2n) для неограниченных алфавитов. Улучшенная предобработка образца в этом методе позволяет использовать суффиксное дерево (построенное с использованием алгоритма Вейнера [Weiner, 1973]), а стадия анализа текста включает нахождение в нем ближайшего общего предка (lowest common ancestor, LCA); Харел и Тарьян [Harel, Tarjan, 1984], Шибер и Вишкин [Schiber, Vishkin, 1988]. Ландау и Вишкин [1986b, 1989] изобрели также другой алгоритм k различий, включающий использование суффиксного дерева. Алгоритм начинает с очень эффективного вычисления матрицы расстояний между строками, после чего отслеживает позиции текста, в которых заканчиваются подстроки, совпадающие с образцом с точностью до k различий. Их методу требуется время O(kn) для алфавитов фиксированной величины и O(n log(m)+kn) для неограниченных алфавитов.
log(m)+kn) для неограниченных алфавитов.
Галил и Джанкарло [Galil, Giancarlo, 1988] придумали, как можно приспособить алгоритм строковых расстояний Машека и Патерсона [Masek, Paterson, 1980, 1983] для решения задачи k различий, чтобы получить время вычислений O(mn/log n). Напоминаем, что при этом подходе требуется, чтобы алфавит был конечным.
Если рассмотреть все упоминавшиеся выше алгоритмы в комплексе, можно сделать следующие наблюдения. Хотя экспоненциальные потребности метода Укконена не позволяют применять его в общем случае, он подходит для очень маленьких образцов, или для маленьких алфавитов и очень маленьких значений k. Для алфавитов фиксированной величины можно видеть, что когда k ограничено 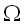 (m/log n), версия алгоритма Машека и Патерсона является асимптотически самой быстрой из всех вышеуказанных методов. (Однако, следует помнить сделанное ранее замечание относительно эффективности алгоритма Машека и Патерсона: он быстрее прямого метода динамического программирования только для очень больших строк). Если же k пропорционально O(m/log n), то следует выбирать алгоритм Ландау и Вишкина [Landau, Vishkin, 1986b, 1989]. Для неограниченных алфавитов их [Landau, Vishkin, 1988] алгоритм быстрее, если k пропорционально O(log1/2m). Однако, алгоритм Ландау и Вишкина [Landau, Vishkin, 1986b, 1989] значительно проще, и он, безусловно, превосходен, когда границей k является
(m/log n), версия алгоритма Машека и Патерсона является асимптотически самой быстрой из всех вышеуказанных методов. (Однако, следует помнить сделанное ранее замечание относительно эффективности алгоритма Машека и Патерсона: он быстрее прямого метода динамического программирования только для очень больших строк). Если же k пропорционально O(m/log n), то следует выбирать алгоритм Ландау и Вишкина [Landau, Vishkin, 1986b, 1989]. Для неограниченных алфавитов их [Landau, Vishkin, 1988] алгоритм быстрее, если k пропорционально O(log1/2m). Однако, алгоритм Ландау и Вишкина [Landau, Vishkin, 1986b, 1989] значительно проще, и он, безусловно, превосходен, когда границей k является 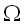 (log1/2m). Заметим, однако, что при больших k, то есть когда k равняется O(m), его эффективность не лучше, чем у адаптации прямого, с квадратичным временем, подхода динамического программирования, предложенной Селлером.
(log1/2m). Заметим, однако, что при больших k, то есть когда k равняется O(m), его эффективность не лучше, чем у адаптации прямого, с квадратичным временем, подхода динамического программирования, предложенной Селлером.
Нечеткое сопоставление применяется, в частности, при исследовании генетических последовательностей. Последовательности ДНК, например, иногда представляют в виде независимых одинаково распределенных символов алфавита {A, C, G, T}. Его буквы представляют nucleotides adenine, cytosine, guanine и thymine соответственно. Аналогично, протеины иногда моделируют как последовательности независимых одинаково распределенных аминокислот; см., например, Сиббалд и Уайт [Sibbald, White, 1987]. Распределение длины самой длинной общей подстроки двух независимых случайных последовательностей исследуется путем сравнения ее с самой длинной серией решек при последовательном бросании монеты. Теоретические результаты были получены как для точного сопоставления [Arratia, Waterman, 1985a], так и для k несовпадений и k различий [Arratia, Waterman,, 1985b]; [Arratia, Gordon, Waterman, 1986].
Родственной сопоставлению строк является задача, допускающая джокеры, символы, которые можно сопоставить с любым символом алфавита, в том числе и с ним самим. (В этом случае будет использоваться термин шаблон, а не образец, как раньше. – Прим. перев.) Пинтер [Pinter, 1985] занимался частным случаем этой задачи, в котором джокеры присутствуют только в шаблоне. Его алгоритм является обобщением процедуры сопоставления строк Ахо-Корасика [Aho, Corasik, 1975]. Последняя является, в свою очередь, обобщением алгоритма Кнута-Морриса-Пратта и ищет составные шаблоны в текстовых строках за время O(m+n), где m – это сумма длин всех шаблонов. На стадии предварительных вычислений в этом алгоритме по множеству шаблонов за время O(m) строится автомат сопоставления шаблонов, похожий на детерминированный конечный автомат, но имеющий две переходные функции. Затем он используется для сканирования текста и одновременного поиска вхождения шаблонов за время O(n). Линейность этого метода обеспечивается в алгоритме Пинтера благодаря тому, что элементы в массиве накапливающих регистров могут приращиваться параллельно; в противном случае временная сложность становится квадратичной.
Случай, когда джокеры могут встречаться как в шаблоне, так и в тексте, исследовали Фишер и Патерсон [Fischer, Paterson, 1974]. Для строк над фиксированным алфавитом  , они показали, что эта задача эквивалентна целочисленному умножению, и, используя умножение Шенхаге-Штрассена [Schonhage, Schtrassen, 1971] (см. тж. книжку Ахо, Хопкрофта и Ульмана [Aho, Hopcroft, Ullman, 1974]), вывели непрямой алгоритм, выполняющийся за время O(n log2 m log log m log
, они показали, что эта задача эквивалентна целочисленному умножению, и, используя умножение Шенхаге-Штрассена [Schonhage, Schtrassen, 1971] (см. тж. книжку Ахо, Хопкрофта и Ульмана [Aho, Hopcroft, Ullman, 1974]), вывели непрямой алгоритм, выполняющийся за время O(n log2 m log log m log  ). Однако, постоянным членом этого сложного выражения нельзя пренебречь, поэтому этот алгоритм представляет практический интерес только для случая очень длинных строк. Для неограниченных алфавитов до сих пор не известны алгоритмы, эффективность которых превосходит квадратичную эффективность наивного метода.
). Однако, постоянным членом этого сложного выражения нельзя пренебречь, поэтому этот алгоритм представляет практический интерес только для случая очень длинных строк. Для неограниченных алфавитов до сих пор не известны алгоритмы, эффективность которых превосходит квадратичную эффективность наивного метода.
К настоящему времени разработано множество разнообразных технических средств для приложений задачи сопоставления строк, таких, как текстовый поиск в больших неформатированных наборах документов. В них применяются методы, использующие клеточные массивы (cellular arrays) [Hollaar, 1979; Foster, Kung, 1980; Mukhopadhyay, 1980; Curry, Mukhopadhyay, 1983; Halaas, 1983; Lee, Mark, 1989], ассоциативную память [Burkovski, 1982; Lee, lochovsky, 1985], конечные автоматы [Hollaar, 1979; Haskin, 1981; Robert, 1982; Haskin, Hollaar, 1983] и динамическое программирование [Hall, Dowling, 1980; Salton, 1980; Yanilos, 1983].
В частности, одно из устройств SMOS VLSI, разработанное совсем недавно в NEC [Yamada et al., 1987; Hirata et al., 1988], сочетает логику конечных автоматов (FSA) с ассоциативной памятью (CAM), и позволяет производить нечеткое сопоставление строк. 512-символьные (16-битные) CAM можно конфигурировать так, чтобы они содержали от 64 8-символьных до 1 512-символьного шаблонов строк. Последовательные входные данные со скоростью 10 миллионов символов/с подаются через CAM, которая выполняет параллельное сопоставление и подает сигналы сопоставления (match signals) логике FSA. Помимо точного сопоставления строк, режим нечеткого сопоставления позволяет отслеживать встречаемости образца с точностью до 1 различия. Имеется также режим с переменным количеством последовательно идущих универсальных символов, в котором ищется строка, начинающаяся и заканчивающаяся заданными символами, с переменным числом произвольных символов между ними. И наконец, режим маскировки (mask mode) разрешает универсальное сопоставление при вводе данных, что позволяет, например, кодировать нераспознанные символы, поступающие из системы OCR (оптическое распознавание символов), и считать их сопоставимыми с любым символом образца.
Задача нахождения самой длинной подстроки (longest repeated substring), появляющейся в данной строке более одного раза, можно сформулировать следующим образом.
 0, |v|
0, |v| 0 и |w|
0 и |w|  0.
0.Максимальная повторяющаяся подстрока – это подстрока, имеющая в данной строке не меньше двух различных вхождений, причем сопоставление нельзя продолжить ни в одном направлении. Рассмотрим, например, строку PABCQRABCSABTU. Подстроки A, B, C, AB, BC и ABC повторяются. Строки AB и ABC являются максимальными повторяющимися подстроками, и, таким образом, ABC является самой длинной повторяющейся подстрокой.
Наивный подход к решению этой задачи, которому требуется квадратичное время, состоит в следующем. Строится матрица M размерности n n, такая что Mi,j = 1 если yi = yj, и Mi,j = 0 в противном случае. За исключением главной диагонали, все диагонали в матрице, состоящие из идущих подряд `1’, представляют максимальные повторяющиеся подстроки, самая длинная из которых является, таким образом, самой длинной повторяющейся подстрокой. Обратите внимание, что матрица симметрична относительно главной диагонали, поэтому достаточно вычислять и обрабатывать только одну, скажем, верхнюю, ее половину (то есть элементы M1...n-1,i+1...n+1).
n, такая что Mi,j = 1 если yi = yj, и Mi,j = 0 в противном случае. За исключением главной диагонали, все диагонали в матрице, состоящие из идущих подряд `1’, представляют максимальные повторяющиеся подстроки, самая длинная из которых является, таким образом, самой длинной повторяющейся подстрокой. Обратите внимание, что матрица симметрична относительно главной диагонали, поэтому достаточно вычислять и обрабатывать только одну, скажем, верхнюю, ее половину (то есть элементы M1...n-1,i+1...n+1).
Однако, самую длинную повторяющуюся подстроку можно найти за линейное время, если использовать одну из структур данных, предложенных Вейнером (Weiner, 1973), содержащих компактный индекс для всех различных подстрок строки. Этот индекс активно исследовался, выступая под следующими названиями:
Patricia trees [Morrison,1968]
Position trees [Aho, Hopcroft and Ullman, 1974; Majster and Reiser, 1980]
Suffix trees [McGreight, 1976; Rodeh, Pratt and Even, 1981; Crochemore, 1986]
Complete inverted files [Blumer et al., 1984a, 1984b, 1985, 1987]
Subword trees [Apostolico, 1985]
Впервые этот индекс упоминается (хотя и в неявной форме) в структуре Patricia trees Моррисона. Однако, самым первым эту структуру использовал Вейнер (Weiner), точное толкование его конструкции дано Ченом и Сейферасом [Chen, Seiferas, 1985]. Интерактивная конструкция Мейстера и Рейзера [Majster, Reiser, 1980] позволяет строить индекс в процессе посимвольного ввода строки слева направо. Апостолико [Apostolico, 1985] анализирует несколько приложений индекса в форме суффиксного дерева Мак-Крейта (McCreight), такие, как нахождение самых длинных общих подстрок и алгоритмы для выполнения сжатия последовательных данных за линейное время. Основная идея последнего состоит в том, что построение суффиксного дерева перемежается с синтаксическим разбором текстовых строк и формировании фраз. Роде, Пратт и Ивен [Rodeh, Pratt, Even, 1981], например, использовали суффиксные деревья для реализации оптимальных универсальных методов сжатия данных Зива и Лемпеля [Ziv, Lempel, 1977].
Построение суффиксных деревьев и их приложение к данной задаче более подробно описывается в следующей главе.
И, наконец, одна из разновидностей этой задачи состоит в отыскании всех максимальных повторяющихся подстрок заданной строки. И снова, наивный подход позволяет решить эту задачу за квадратичное время. Однако Бейкер [Baker, 1992] исследовала применение суффиксных деревьев для этой задачи. Она разработала программный инструмент визуализации вхождений повторяемых или родственных секций кода в больших программных системах. Строки кода, из которых убраны комментарии и пробелы, рассматриваются как символы составной строки, а для того, чтобы отфильтровать тривиальные повторы, можно установить пороговое значение минимальной длины повторяющихся подстрок. Метод основан на построении суффиксных деревьев Мак-Крейта (McCreight), и весь алгоритм выполняется за время O(n+r), где r – число найденных пар максимальных повторяющихся подстрок (которое обычно мало по сравнению с n).