|
|
|
|
Эта глава посвящена более подробному описанию алгоритмов, в общих чертах охарактеризованных в предыдущей главе.
Все подстроки текста y(i, i+m-1), 1
in-m+1, последовательно сопоставляются с образцом x, пока не встретится первое вхождение образца или не будет достигнут конец текста.
i = 1 - инициализация индекса y j = 1 - инициализация индекса x while (i
Рис. 4.1: Сопоставление строк наивным методом
При каждом i сравниваются не более m символов, так что суммарное количество проверок не превосходит m
(n-m+1). Количество сравнений максимально, когда каждая подстрока отличается от образца лишь последним символом (с номером m); последняя подстрока может и совпасть с образцом. Вот пример:
x = EEEEW y = EEEEEEEEEEEEEEEEEEEEEEEW
Однако на практике подобные ситуации встречаются редко. Средняя эффективность равна O(m+n), так как отвергающие символы, как правило, стоят не на последнем месте, а гораздо раньше (символ образца называется отвергающим, если в процессе сопоставления он не совпал с очередным символом текста; с тем же основанием отвергающим называется и соответствующий символ текста). Разумеется, реальная эффективность метода зависит от реальных свойств – как образца, так и текста.
Псевдокод, реализующий наивный подход, приведен на рис. 4.1. В самом начале i и j, индексы образца и текста соответственно, указывают на начала, они увеличиваются на 1 на каждом шаге, если стоящие в этих позициях символы совпадают. В противном случае индексы переустанавливают, и j снова указывает на начало образца, а i – на первую позицию следующей проверяемой подстроки. Если найдена подстрока текста, совпадающая с образцом, i укажет ее начало в тексте, если же достигнут конец текста, а нужная подстрока так и не встретилась, индекс i будет равен нулю.
Подход Кнута, Морриса и Пратта близок к наивному, но обладает по сравнению с ним неоспоримым преимуществом: индекс i, нумерующий символы текста, не уменьшается. Это достигается тем, что в случае провала сопоставления образец сдвигается относительно текста на величину, зависящую от его структуры и от номера символа, на котором это произошло. Величина сдвига задается таблицей next из m элементов, которая вычисляются на предварительном этапе при анализе образца.
Алгоритм поиска представлен на рис. 4.2. Если несовпадение между текстом и образцом обнаружено в позициях i и j соответственно, то мы знаем, что предыдущие j-1 символов текста совпадают с первыми j-1 символами образца, т.е. подстрока y(i-j+1, i-1) совпадает с префиксом x(1, j-1). Эта информация и отражена в таблице next. Ее j-й элемент nextj указывает, какое положение образца использовать при следующей попытке сопоставления, если j-й элемент образца оказался отвергнутым.
i = 1 - инициализация индекса текста y j = 1 - инициализация индекса образца x while (iОбратите внимание на то, что and во внутреннем цикле является условным: его правый операнд вычисляется только в том случае, если значением левого является истина.yi) j = nextj i = i + 1 j = j + 1 if j > m i = i - m else i = 0
Во внутреннем цикле мы присваиваем j значение nextj, что равносильно сдвигу образца на j-nextj символов вправо относительно текста. Цикл останавливается, когда либо j = 0, либо xj = yi. В первом случае никакая часть x не совпадает с текущей подстрокой текста; во втором префикс x(1,j) совпадает с подстрокой y(i-j+1,i). Затем внешний цикл возобновляется приращением индексов текста и образца. Если обнаружено полное совпадение, то i укажет на первую позицию вхождения x в y, в противном случае i = 0.
Основой алгоритма является таблица next. Рассмотрим сначала ее упрощенную версию, которую проиллюстрируем следующим примером.
j 1 2 3 4 5 6 7 8 xj A B C D A B C E nextj 0 1 1 1 1 2 3 4
Отсюда видно, что если при попытке сопоставления указанного выше образца с данной строкой текста отвергающим оказался, скажем, символ j = 8, то следующим с текущим символом текста нужно сравнивать символ x4. Эта ситуация иллюстрируются ниже.
Попытка сопоставления провалилась при сравнении yi и x8:
j = 8 образец A B C D A B C E текст . . . A B C D A B C D . . .
На следующем шаге сравниваются символы yi и x4.
j = 4 образец A B C D A B C E текст . . . A B C D A B C D . . .
Значения элементов таблицы next можно получить, основываясь на следующих соображениях. Если отвергающими оказались символы xj и yi, то мы знаем, что x(1, j-1) совпадает с y(i, i+j-1). Предположим теперь, что у подстроки x(1, j-1) имеются равные друг другу префикс и суффикс, длины, скажем, k-1. Легко видеть, что в этом случае перед продолжением поиска образец x можно сдвинуть так, чтобы префикс занял место, прежде занимаемое суффиксом. Таким образом, на следующем шаге с текущим символом текста будет сравниваться символ xk образца, расположенный сразу же за префиксом. Поскольку мы заинтересованы в возможно больших сдвигах, нужно выбирать префикс максимально возможной длины. На случай несовпадения в первом символе образца, next1 содержит значение 0, указывающее, что весь образец следует продвинуть «за» символ yi.
Итак, nextj равняется максимальному из целых k, которые обладают следующими двумя свойствами: (a) k < j, и (b) префикс и суффикс образца длины k-1 равны другу, т.е. x(1, k-1) = x(j-k+1, j-1). Если таких префикса и суффикса нет (т.е. x(1, k-1) = 
), то k берется равным 1. Значение k можно получить следующим образом. Будем сравнивать строку x(1, j-1) саму с собой, продвигая одну ее копию над другой слева направо. Начнем с положения, когда первое сравнение проводится между x1 и x2, и остановимся, либо когда перекрывающиеся отрезки равны друг другу, либо когда не останется символов для сравнения. Перекрывающиеся отрезки в этом случае и задают требуемый префикс, а k равно его длине плюс 1.
Возвращаясь к предыдущему примеру, проиллюстрируем ситуацию для next8.
A B C D A B C x(1,7) A B C D A B C
Мы видим, что здесь перекрываются 3 символа. Поэтому в данном случае значение next8 равно 4.
Обратите внимание, что в процедуре поиска, сразу же после приращения, j равно максимальному целому числу, которое не превосходит i, и для которого выполнено x(1, j-1) = y(i-j+1, i-1). Если в этом выражении y заменить на x, оно полностью совпадет с описанным выше определением значений таблицы next. Таким образом, метод генерации таблицы next похож на саму процедуру поиска, с тем отличием, что в нем образец сопоставляется сам с собой. Его псевдокод дан на рисунке 4.3.
И снова and во внутреннем цикле является условным.j = 1 k = 0 next1 = 0 - специальное значения для случая несовпадения с x1 while j < m while (k > 0) and (xj
Как уже говорилось, приведена упрощенная версия таблицы next. В ней учитывается не вся доступная информация: незадействованным остается символ, вызвавший несовпадение. Рассмотрим предыдущий пример. Если несовпадение возникает, скажем, между yi и x7 (вторым C), то следующими, согласно этой таблице, будут сопоставляться yi и 
, то есть x3 (первое C). Однако это сравнение также не будет успешным, и next сместит сравнение к x1. Усовершенствованная таблица next в случае несовпадения по x7 сразу перейдет к сравнению с x1. Поэтому модифицированное определение nextj выглядит следующим образом: это значение должно быть равно максимальному k, меньшему j, при котором x(1, k-1) = x(j-k+1, j-1) и xjxj, если же такого k нет, nextj = 0. Новая таблица next, построенная в соответствии с этим определением, приведена ниже.
j 1 2 3 4 5 6 7 8 x A B C D A B C E next 0 1 1 1 0 1 1 4
Это улучшение легко реализовать, изменив способ вычисления nextj в алгоритме построения таблицы next, окончательная версия которого дается на рисунке 4.4. Теперь, если xj = xk, то nextj присваивается значение nextk. Это гарантирует, что в случае несовпадения текущий символ текста не будет сравниваться с символом образца, совпадающим с только что забракованным.
Как всегда and во внутреннем цикле является условным.j=1 k=0 next1 = 0 - специальное значение: отвергающим оказался символ x1 while j < m while (k > 0) and (xj
Алгоритм поиска, представленный на рисунке 4.2, обладает интересным свойством: общее количество выполняемых во внутреннем цикле присваиваний j = nextj не превосходит количества присваиваний в операции приращения i во внешнем цикле. Таким образом, во внутреннем цикле образец сдвигается вправо не больше n раз, что дает время сопоставления O(n). Аналогично, можно показать, что следующий этап инициализации таблицы next выполняется за время O(m). Итак, общее время для худшего случая равно O(n+m) и не зависит от размера алфавита символов.
Этот максимум по времени достигается в задаче сопоставления образца строки Фибоначчи. Кроме того, было показано, что максимальное число раз, которое внутренний цикл может выполниться, оставаясь на одной и той же позиции в тексте равно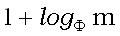 
, где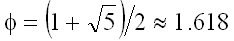 
– число, известное как золотое сечение (Кнут, Моррис и Пратт [Knuth, Morris, Pratt, 1977]).
Средняя эффективность алгоритма для случайных строк анализировалась Бейза-Ейтсом [Baeza-Yates, 1989b]. Для алфавитов 
, удовлетворяющих условию 
> 
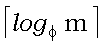, была выведена верхняя граница ожидаемого числа сравнений символов An, улучшающая полученный ранее результат (Рейнер [Regnier, 1988]):
.
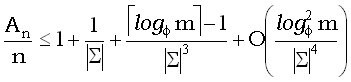Например, числовое значение этой границы для образца длиной 10 и алфавита из 256 символов приближенно равно 1.004n. Любопытно, что для тех же параметров и больших n примерно такую же эффективность дает наивный метод, для которого оценку значения An получил Бейза-Ейтс (Baeza-Yates, 1989b).
.
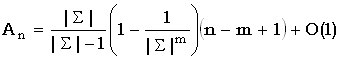В работе Кнута, Морриса и Пратта [Knuth, Morris, Pratt, 1977] вы найдете различные соображения о том, как можно еще улучшить эффективность. Например, специальные символы (стражи) в конце строки позволяют не следить за границами индекса. Кроме того, таблицу next можно использовать для компиляции конечного автомата, сопоставляющего с образцом. Кроме того, они рассмотрели разнообразные расширения задачи, такие, как поиск всех вхождений образца.
В алгоритме Бойера-Мура образец движется вдоль строки текста слева направо, однако фактические сравнения символов выполняются справа налево. Первыми, таким образом, сравниваются символы xm и ym. Если они не совпадают и ym не встречается нигде в x, мы можем спокойно сдвинуть образец на m символов вправо, так как можем быть уверены, что ни одна из начинающихся с одной из первых m позиций подстрок не совпадает с образцом. Следующими сравниваются xm и y2m.
Пусть отвергающими оказались символы xm и yi. Как уже говорилось, если yi не содержится нигде в образце, шаблон можно сдвинуть на m позиций вправо. С другой стороны, если yi присутствует в образце, и xm-s – его самое правое вхождение, то образец можно сдвинуть лишь на s позиций вправо, совмещая xm-s с yi. Проверку можно продолжить сравнением xm с yi+s, то есть текстовый индекс мы увеличиваем на s.
Если xm и yi совпадают, нужно сравнивать предшествующие им символы в образце и тексте, пока вся подстрока текста не будет сопоставлена с образцом или пока не встретится несовпадение. Если отвергающим оказался, скажем, символ xj, то мы знаем, что суффикс x(j+1,m) равен подстроке текста y(i-m+j+1, i), и xjyi-m+j. Теперь, если самым правым вхождением yi-m+j в образец снова является, скажем, xm-s, образец можно сдвинуть на j-m+s мест вправо, так что xm-s окажется на одной позиции с yi-m+j. Процедуру можно продолжить сравнением xm с соответствующим символом, в данном случае с yi+j-m+s. Приращение индекса текста с позиции несовпадения до следующей пробной позиции равно, таким образом, (i+j-m+s)-(i-m+j) = s. Обратите внимание, что приращение то же, что и в предыдущем случае.
Если xm-s находится правее xj, то значение j-m+s отрицательно, так что совмещение xm-s с yi-s+j ничего не даст, поскольку повлечет за собой шаг назад. В этих обстоятельствах образец лучше сдвинуть на одно место вправо и сравнивать xm с yi+1. Для этого нужно увеличить индекс текста на (i+1)-(i-m+j) = m+1-j.
Приращения s, используемые в эвристике вхождения, вычисляются заранее и хранятся в таблице skip (Бойер и Мур использовали обозначение delta1 [Boyer, Moore, 1977]). В процессе поиска таблица индексируется отвергающими символами текста, поэтому требуется таблица размером с используемый алфавит символов. Вход для символа w равен m-j, где xj – самое правое вхождение w в x, и равен m, если w не содержится в x, то есть:
skip[w] = min {s : s = m или (0s < m и x[m-s] = w)}
Таблица skip для алфавита инициализируется следующим образом:
for w = 1 to
Отсюда видно, что время инициализации skip-таблицы равно O(m+).
Вот пример, иллюстрирующий работу skip-таблицы для образца ABCDB.
w A B C D E F G H ... skip[w] 4 0 2 1 5 5 5 5 ...
Несовпадение возникает при yi = A
образец A B C D B текст . . . L M N A B C D B . . . i
Следующими сравниваются символы xm и yi+skip[A], то есть yi+4.
образец A B C D B текст . . . L M N A B C D B . . . i i+4
Если, как в описанном выше случае, несовпадение встречено уже после того, как найдено частичное совпадение, иногда можно продвинуться дальше, чем позволяет эвристика вхождения. Если это так, лучше взять больший сдвиг, определяемый эвристикой сопоставления. При этом используется таблица, похожая на используемую в алгоритме Кнута-Морриса-Пратта. Идея состоит в том, что в результате сдвига символы образца должны быть равны всем тем символам текста, с которыми они совпадали перед этим, а на месте отвергающего символа должен оказаться другой. Последнее условие было независимо предложено Куперсом (Kuipers) (отмечено в работе Бойера и Мура [Boyer, Moore, 1977]) и Кнутом (постскриптум в работе Кнута, Морриса и Пратта [Knuth, Morris, Pratt, 1977]). Это усовершенствование исходной эвристики Бойера и Мура аналогично усовершенствованию таблицы next в алгоритме Кнута-Морриса-Пратта.
Как уже говорилось, особый интерес представляет ситуация, когда часть образца содержится в текущей части текста, т.е. x(j+1, m) = y(i-m+j+1, i) и xjyi-m+j. Если суффикс x(j+1, m) входит также в x как подстрока x(j+1-t, m-t), причем xj-t xj, и это самое правое из подобных вхождений, то образец можно сдвинуть на t мест вправо. При этом мы совмещаем x(j+1-t, m-t) с y(i-m+j+1, i) и процесс поиска можно возобновить, сравнивая xm с yi+t. Таблица shift (обозначена Бойером и Муром [Boyer, Moore, 1977] как delta2), содержащая информацию о сдвиге t, вычисляется заранее на основании образца и индексируется той позицией образца, в которой встретилось несовпадение. Значение shift[j] равняется сдвигу t образца плюс дополнительный сдвиг, требуемый для того, чтобы возобновить сравнения от правого края образца. Значение i – это минимум, такой что, если xjyi-m+j, то x(j+1-t, m-t) совпадет с y(i-m+j+1, i). Итак, входы таблицы shift определяются следующим выражением:
shift[j] = min{t + m - j : t
1 и
(tj или xj-txj) и
((tk или xk-t = xk) для j < km)}
Таким образом, значение shift[j] равно требуемому приращению для индекса текста с текущей позиции yi-m+j до позиции следующего сравнения yi+t, то есть (i + t) - (i - m + j) = t + m - j. Вот пример, иллюстрирующий значения shift для образца ABCDABC.
xj A B C D A B C j 1 2 3 4 5 6 7 m - j 6 5 4 3 2 1 0 t 4 4 4 4 7 7 1 shift[j] 10 9 8 7 9 8 1
Из определения shift[j] можно углядеть, что shift[j]m+1-j. Так, в указанном выше случае, где индекс текста следует увеличить на m+1-j, вместо соответствующего значения shift, так как последнее вызывает сдвиг образца назад, достаточно использовать соответствующее значение таблицы shift. Таким образом, в случае несовпадения следует использовать максимальное из двух значений, взятых из описанных выше таблиц. Алгоритм для этого метода представлен на рисунке 4.5. Конечное значение i возвращает позицию вхождения образца в тексте, или 0, если образец в тексте не встретился.
i = m j = m while (j > 0) and (iНа рисунке 4.6 представлен способ вычисления таблицы shift. Этот метод, описанный Ахо [Aho, 1990], создан Кнутом (Knuth, Morris, Pratt, 1977) и модифицирован Мелхорном (Mehlhorn) [Smit, 1982]. Промежуточная функция f, вычисляемая в алгоритме, определяется так: f[m] = m+1, и f[j] = min{i : j < i
Как обычно, and во втором цикле while является `условным’.for i = 1 to m shift[i] = 2 * m - i j = m k = m + 1 while j > 0 f[j] = k while (k
Рис. 4.6: Инициализация таблицы shift для алгоритма Бойера-Мура
Кнут продемонстрировал, что для локализации всех вхождений образца в текст алгоритму Бойера-Мура требуется O(n+rm) сравнений символов, где r – число вхождений (Knuth, Morris, Pratt, 1977). Он показал также, что в случае отсутствия в тексте образца требуется всего 6n сравнений символов. Для больших алфавитов средняя эффективность алгоритма Бойера-Мура является сублинейной, и в среднем требует n/m сравнений символов.
Вариант алгоритма Бойера-Мура, предложенный Апостолико и Джанкарло [Apostolico, Giancarlo, 1986], локализации всех вхождений образца требует максимум 2n-m+1 сравнений символов. Сопутствующие вычисления несколько менее обременительны, однако тоже линейны по m. Применяемый метод использует информацию о том, какая подстрока образца совпала с какой подстрокой текста в предыдущих пробных позициях, и использует упрощенную форму определения таблицы shift.
Существует множество других вариантов подхода Бойера-Мура к сопоставлению строк. Один из наиболее известных, алгоритм Бойера-Мура-Хорспула, с упрощенными предварительными вычислениями, описан в следующем разделе.
4.1.4. Бойер-Мур-Хорспул
На практике эвристика сопоставления в алгоритме Бойера-Мура мало влияет на общую скорость поиска. Она полезна в случае образцов с большим числом повторов, которые, однако, редко встречаются в реальных приложениях. Включение этой эвристики позволяет добиться в худшем случае линейной эффективности, а не O(mn).
Хорспул [Horspool, 1980] разработал упрощенную версию алгоритма Бойера-Мура, в которой отказался от эвристики сопоставления и использует только эвристику вхождения. Это сокращает объем предварительных вычислений, а также снижает требования к памяти с O(m+
Таблица skip в версии Хорспула слегка отличается от используемой в версии Бойера-Мура: в ней skip[xm] присваивается значение m, так что остается инициализировать только элементы с x1 до xm-1. В таблице Бойера-Мура значение skip для xm равно 0, а ненулевой сдвиг определяется взятием максимума из значений двух эвристик – сопоставления и вхождения.
Хорспул отметил также, что, в случае несовпадения, скажем, в xj, в качестве следующей пробной позиции можно взять такую, что любой из m-j сопоставляемых символов текста совмещается с самым правым вхождением этого символа в образце. Всегда используя для индексации таблицы skip символ текста, соответствующий последнему символу образца (xm), можно избежать описанной выше ситуации с обратным сдвигом образца. Иначе данная ситуация потребовала бы явной проверки. Вспомним, что в алгоритме Бойера-Мура для борьбы с этой ситуацией предназначена эвристика сопоставления. Алгоритм Бойера-Мура-Хорспула представлен на рисунке 4.7. И снова, окончательное значение i содержит первую позицию вхождения образца, или равно 0, если образец в тексте не обнаружен.
Бейза-Ейтс [Baeza-Yates, 1989a] показал, что среднее число An сравнений символов, выполняемых алгоритмом Бойера-Мура-Хорспула для случайных строк, ограничено снизу следующим выражением:
(4.5)
Для образца длины 10 и алфавитов, размеры которых равны 10, 100 и 256, приведенное выражение дает, соответственно, 0.17, 0.11 и 0.10 – на эти коэффициенты нужно умножить (n-m+1). Отсюда видно, что для больших алфавитов нижняя граница близка к (n-m+1)/m в среднем случае, то есть при n
m примерно равна n/m.
Как и всюду, and во внутреннем while является `условным’.- инициализация таблицы skip for w = 1 to |C| skip[w] = m for j = 1 to m - 1 skip[xj] = m - j - поиск i = m j = m while (j > 0) and (i
Рис. 4.7: Сопоставление строк по Бойеру-Муру-Хорспулу4.1.5. Сандей: Быстрый поиск, Максимальный сдвиг, Оптимальное несовпадение
Сандей [Sunday, 1990] обнаружил, что в алгоритме Бойера-Мура при обнаружении несовпадения, когда xm совмещен с i-м символом текста, для обращения к таблице эвристики сопоставления вместо yi можно использовать следующий символ, то есть yi+1. Основанием для этого является то, что при минимальном сдвиге образца, то есть на один символ вправо, yi+1 является частью следующей проверяемой подстроки текста. Сандей утверждает, что на практике в среднем это дает сдвиг, больший или равный сдвигу на значение skip Бойера-Мура плюс один. Однако, даваемое этим фактом преимущество в скорости уменьшается с увеличением длины образца.
И опять and во внутреннем цикле while является `условным’.- инициализация таблицы skip for w = 1 to |C| skip[w] = m + 1 for j = 1 to m skip[xj] = m + 1 - j - поиск i = 1 j = 1 while (j
Рис. 4.8: Быстрый поиск по Сандею
Смит [Smith, 1991] отметил, что в некоторых ситуациях yi использовать выгоднее, чем yi+1, что и показано в приведенном ниже примере для образца ABCDE. Поэтому он предложил использовать максимальную из эвристик сопоставления этих двух символов.
Таблица skip Бойера-Мура для образца ABCDE
w A B C D E F G H . . . skip[w] 4 3 2 1 0 5 5 5 . . . Несовпадение возникает в yi = T
образец A B C D E текст . . . P Q R S T D U V W X . . . iСледующая позиция образца основывается на skip[yi], то есть i + skip[T]
образец A B C D E текст . . . P Q R S T D U V W X . . . i+5 Следующая позиция образца основана на skip[yi+1], то есть i + skip[D] + 1
образец A B C D E текст . . . P Q R S T D U V W X . . . i+2 Сандей заметил также, что символы образца и текущей подстроки текста можно сравнивать в любом порядке и использовал этот факт для улучшения общей эффективности. Он предложил три различных варианта поиска Бойера-Мура. Все они используют yi+1 в эвристике вхождения, но различаются порядком сравнения символов. Сандей высказал гипотезу, что линейное поведение алгоритма Бойера-Мура в худшем случае сохраняется при произвольном порядке сравнения символов подстрок.
Самым простым из предложенных является алгоритм Быстрый Поиск, в котором сравнения выполняются строго слева направо и применяется только эвристика сопоставления. Псевдокод приведен на рисунке 4.8. Обратите внимание, что для учета дополнительной позиции сдвига образца таблица skip инициализируется значениями, на 1 большими, чем значения таблицы Бойера-Мура.
В двух других методах – алгоритмах Максимальный сдвиг и Оптимальное несовпадение – используется дополнительный массив, где хранятся индексы образца, причем в том порядке, в котором сравниваются символы образца и текста. В процессе поиска производится последовательное обращение к этому массиву, и таким образом обеспечивается желаемый порядок символов в образце.
В алгоритме Максимальный сдвиг сравнения производят в порядке, максимизирующем значения сдвига в эвристике сопоставления. Для этого символы сортируют в порядке убывания их расстояния до следующего вхождения, а если символ не повторяется – до начала образца. Таким образом, если образец не содержит повторяющихся символов, сравнения производятся последовательно справа налево.
В последнем алгоритме, при поиске оптимального несовпадения в целях более раннего выявления несовпадения первыми сравнивают более редкие символы. Для этого символы образца сортируют в порядке убывания их частоты в тексте, поэтому необходимо априорное знание этой статистики. Полные реализации алгоритмов Максимальный сдвиг и Оптимальное несовпадение на Си можно найти у Сандея [Sunday, 1990].
Сандей обнаружил, что самым быстрым из трех алгоритмов является Оптимальное несовпадение, и сообщил, что все они превосходят по средней эффективности алгоритм Бойера-Мура; так, для алгоритма Оптимальное несовпадение сообщается о выигрыше в скорости на 10-20%. Различия в скорости, однако, уменьшаются по мер увеличения длины образца, что согласуется с обычным поведением при использовании символа текста, следующего за отвергающим.
Кроме того, эмпирическое сравнение алгоритмов Сандея с упрощенной версией алгоритма Бойера-Мура проводил Пирклбауер [Pirklbauer, 1992]. Он обнаружил, что если учитывать время предварительных вычислений, то для длинных строк процедуры Максимальный сдвиг и Оптимальное несовпадение обходятся довольно дорого. Издержки на предварительные вычисления весьма значительны, особенно если ищется только первое вхождение образца. Алгоритм Быстрый поиск, однако, был рекомендован к использованию – из-за эффективности, близкой к эффективности варианта Бойера-Мура, и легкости в реализации.
Смит [Smith, 1991] постарался преодолеть недостаток метода Оптимальное несовпадение, а именно требование предварительного знания статистик входного текста. Его адаптированный метод начинает с произвольного порядка сравнения символов, который затем модифицируется в процессе поиска. Алгоритм обходится без эвристики сопоставления, и использует только эвристику вхождения. Оказалось, что эта модель, не зависящая от языка, в среднем работает не намного хуже, чем эквивалентный ей поиск, основанный на статическом языке, то есть версия алгоритма Оптимальное несовпадение, использующая только эвристику вхождения. Метод, используемый для адаптации упорядочения, состоит в том, чтобы передвигать символ, вызвавший несовпадение, либо на одну позицию вверх, либо к верху списка, придавая ему, таким образом, более высокий приоритет в будущих попытках сопоставления. Как упоминалось ранее, метод Смита включает также выбор максимального из двух значений сдвига эвристики вхождения – одно для выровненного по концу образца символа текста, а другое для следующего символа текста.
4.1.6. Хьюм и Сандей. Улучшенные алгоритмы Бойера-Мура и Наименьшая цена
При обсуждении эффективности Бойер и Мур [Boyer, Moore, 1977] представили реализацию своего алгоритма с ‘быстрым’ skip-циклом, включающим только эвристику вхождения. Идея состоит в том, чтобы быстро покончить с несовпадениями, и только после того, как произведено успешное сопоставление с xm, первым тестируемым символом образца, запустить ‘медленный’ цикл, в котором с текстом сравниваются остальные символы образца. Если несовпадение выявляется на этой стадии, то для определения следующего пробного положения образца используется большая из двух эвристик вхождения, после чего возобновляется поиск в быстром цикле.
Хьюм и Сандей [Hume, Sunday, 1991] представили таксономию родственных алгоритмов, основанные на подходе Бойера-Мура. Рассматривались три отдельных компоненты этой процедуры, а именно: быстрый skip-цикл, медленный цикл сопоставления и вычисление сдвига образца до следующей пробной позиции в случае несовпадения внутри медленного цикла.
Для каждой из трех компонент рассматривались различные методы. Например, исследовались последствия выбора разных символов образца для первоначальной проверки в skip-цикле: x1, xm и самый редкий из символов текста. Для цикла сопоставления исследовались разные порядки сравнения – например, слева направо, справа налево, а также Максимальный сдвиг и Максимальное несовпадения Сандея. Во всех случаях, кроме Оптимального несовпадения, перед полным сопоставлением проводилось отдельное сравнение, в котором использовался символ образца с низкой встречаемостью. На стадии вычисления сдвига использовались таблицы Кнута-Морриса-Пратта, эвристики Бойера-Мура и таблицы сдвига Сандея, а также их комбинации. Было обнаружено, однако, что преимущества объединения эвристик перевешиваются расходами на определение максимальных значений.
На основании экспериментов, проводимых с текстами из Библии, для каждой из трех стадий были выявлены наиболее эффективные методы, и предложены две новые процедуры, а именно, улучшенный алгоритм Бойера-Мура и алгоритм Наименьшая цена. Оба используют предваряемое отдельным сопоставлением сравнение слева направо для цикла сопоставления и версию эвристики сопоставления Сандея для вычисления сдвига при несовпадении в цикле сопоставления. Они различаются методами, используемыми в skip-цикле: улучшенный алгоритм Бойера-Мура использует оптимизированную версию исходного ‘быстрого’ цикла Бойера-Мура, в то время как алгоритм наименьшей цены сначала ищет символ образца с наименьшей ценой поиска. Она определяется встречаемостью символов в тексте и положением символа внутри образца, влияющим на размер возможного сдвига.
Реализации этих двух алгоритмов на Си имеются у Хьюма и Сандея [Hume, Sunday, 1991], где, кроме того, даются инструкции, как получить полные копии программ и используемых наборов данных через интернет, ftp или по электронной почте.
Сообщается о превосходстве в 4.5 раз скорости алгоритма Улучшенный Бойера-Мура и Наименьшей цены над скоростью исходного алгоритма Бойера-Мура (не в версии с ‘быстрым циклом’). Обратите внимание, что метод Наименьшей цены использует априорную информацию о встречаемости символов в тексте. Кроме того, следует указать, что, как и у Сандея [Sunday, 1990], алгоритмы сравнивались на задаче локализации всех вхождений образца в текст, издержки предварительных вычислений не учитывались, и тестировались относительно маленькие образцы (с длиной m
4.1.7. Харрисон
Хотя метод Харрисона (Harrison) и решает не в точности ту задачу сопоставления строк, которая определена выше, мы все же приводим его здесь, так как он дает эффективный способ исключения текстов, в которых вероятность встретить образец очень мала. Обратите внимание, что этот метод требует предобработки текста.
Основная идея состоит в том, что строки представляются более простыми объектами, сохраняющими некоторые из присущих этим строкам свойств. В этом методе строка представляется множеством подстрок фиксированной длины, скажем, k. Применяется подходящая хеш-функция, отображающая множество
Необходимым условием присутствия образца в тексте является требование, чтобы xsig, сигнатура образца, являлась подмножеством сигнатуры текста ysig. Если подстрока образца не встречается в тексте, то сам образец тем более не встречается в нем. Это означает, что если xsig содержит ‘1’ в позиции, где в ysig она отсутствует, можно сделать вывод, что x не является подстрокой y. Этот тест можно проводить с помощью логических операторов на двух сигнатурах. Ненулевой результат побитового «И» для xsig и отрицания ysig означает, что успешное сопоставление невозможно. Если же получен нулевой результат, потребуется провести поиск, чтобы определить, встречается ли образец в тексте.
Таким образом, этот метод можно использовать, чтобы быстро отбрасывать строки текста, в которых образец заведомо не может встретиться. Строки большого текстового файла можно, например, хранить вместе с их хешированными k-сигнатурами, что облегчит впоследствии поиск.
4.1.8. Карп-Рабин
В алгоритме Карпа-Рабина, как и в наивном методе, с образцом сопоставляются m-символьные подстроки текста, y(i, i+m-1), для 1
Сигнатуры для x(1,m) и y(1,m) вычисляются заранее, а разумный выбор хеш-функций позволяет в процессе сканирования текста легко выводить сигнатуру для y(i, i+m-1) из сигнатуры для y(i-1, i+m-2). Вот использованная хеш-функция:
h(k) = k mod q (4.6) где q – большое простое число. В вычислениях m-символьные строки трактуются как m-значные целые числа по основанию
ki = yicm-1 + yi+1cm-2 + ... + yi+m-1 (4.7) Число ki+1 для следующей подстроки текста y(i+1, i+m) выводится из ki следующим образом:
ki+1 = (ki - yicm-1)c + yi+m (4.8) Свойство ассоциативности функции mod
(a+b) mod c = (a mod c + b mod c) mod c
позволяет брать остатки после каждой стадии вычислений. Это сохраняет частичные результаты маленькими, и дает тот же результат, который был бы получен, если бы операция mod выполнялась бы только на последней стадии вычислений.
Как и всюду and в утверждении if является ‘условным’.- инициализация i = 1 found = false d = cm-1 mod q hx = (x1 * cm-1 + x2 * cm-2 + ... + xm) mod q hy = (y1 * cm-1 + y2 * cm-2 + ... + ym) mod q - поиск while (i
Рис. 4.9: Сопоставление строк по Карпу-РабинуТак как значения хеш-функции не уникальны, равенство двух сигнатур оказывается необходимым, но не достаточным условием совпадения строк. Поэтому, когда выявлено потенциальное соответствие, две строки надо сравнить напрямую, чтобы проверить, нет ли конфликта сигнатур. Для больших хеш-таблиц шансы такого конфликта невелики. Один из представленных Карпом и Рабином алгоритмов [Karp, Rabin, 1987] еще снижает вероятность большого числа конфликтов, случайным образом перевыбирая q в случае появления конфликта и проводя инициализацию повторно, после чего продолжает поиск. Теоретически в худшем случае на каждой стадии требуется провести m сравнений символов, что дает общее время выполнения O(mn). На практике, однако, можно ожидать, что сигнатуры на каждой стадии будут неравными. В этих обстоятельствах каждая позиция текста обрабатывается постоянное время, что в среднем дает производительность O(m+n). Алгоритм приведен на рисунке 4.9. Обратите внимание, что начальные вычисления hx и hy можно выполнить следующим образом:
hx = 0 for j = 1 to m hx = (hx * c + x[j]) mod q Значение d, используемое для вычисления приращения сигнатуры, первоначально также можно вычислить итеративно, вновь используя ассоциативность операции mod. При вычислении следующей сигнатуры добавляется значение c*q, чтобы частный результат остался положительным. По завершении процедуры поиска i равно первой позиции вхождения образца в тексте, или 0, если образец в тексте не встретился.
Простое число q должно быть как можно большим, однако, таким, чтобы (
