|
|
|
|
В алгоритме k несовпадений Ландау-Вишкина (1985, 1986a) строка текста анализируется с помощью 2-мерной таблицы несовпадений образца (pattern mismatch) pm[1…m-1, 1…2k+1], генерируемой на стадии предварительной обработки образца. Вычисление этой таблицы будет рассмотрено чуть ниже. Сначала мы рассмотрим стадию анализа текста.
При анализе текста используется двумерный массив tm[0…n-m, 1…k+1], содержащий информацию о несовпадениях текста с образцом. По завершении анализа в его i-й строке содержатся позиции в x первых k+1 несовпадений между строками x(1, m) и y(i+1, i+m). Таким образом, если tm[i, v] = s, то yi+s
xs, и это v-е несовпадение между x(1, m) и y(i+1, i+m), считая слева направо. Если число c несовпадений x с подстрокой y(i+1, i+m) меньше k+1, то, начиная с c+1, элементы i-й строки равны значению по умолчанию m+1, то есть:
tm[i, c+1] = tm[i, c+2] = … = tm[i, k+1] = m+1
Обратите внимание: если tm[i, k+1] = m+1, то подстрока y(i+1, i+m) отличается от образца x не более, чем на k символов, и, таким образом, является решением задачи. Это иллюстрируется следующим примером. Рассмотрим случай, когда x = tram, y = thetrippedtrap, а k = 2. Из приведенной ниже таблицы текстовых несовпадений можно видеть, что в тексте найдены вхождения образца с точностью до двух символов, начинающиеся с y4 и y11, а именно, подстроки trip и trap.
|
|
1 |
2 |
3 |
|
0 |
2 |
3 |
4 |
|
1 |
1 |
2 |
3 |
|
2 |
1 |
2 |
3 |
|
3 |
3 |
4 |
5 |
|
4 |
1 |
2 |
3 |
|
5 |
1 |
2 |
3 |
|
6 |
1 |
2 |
3 |
|
7 |
1 |
2 |
3 |
|
8 |
1 |
2 |
3 |
|
9 |
1 |
2 |
3 |
|
10 |
4 |
5 |
5 |
Алгоритм анализа текста приведен на рисунке 4.25. Образец сканируется в цикле for параллельно с текстом слева на права по одному символу за раз. На итерации i с образцом сравнивается подстрока y(i+1, i+m). Самая правая позиция в тексте, достигнутая за предыдущие итерации, задается значением j, то есть j является максимальным из чисел r+tm[r, k + 1], где 0
r < i. Если i < j, вызывается процедура merge, которая находит несовпадения между x(1, j - i) и y(i+1,j) и устанавливает b равным найденному числу. Если оно не превышает k, вызывается процедура extend. Она сканирует текст впереди от y[j + 1], пока либо не будет найдено k + 1 несовпадений, либо не будет достигнуто y[i+m] с не больше чем k несовпадениями, то есть найдено вхождение образца, начинающееся с y[i+1].
Устройство extend довольно очевидно, текст процедуры приведен на рисунке 4.26. Сравниваются пары символов из подстрок y(j + 1, i + m) и x(j - i + 1, m), и в случае несовпадения b увеличивается и таблица текстовых несовпадений обновляется.
- инициализация tm[0 ... n - m, 1 ... k + 1] = m + 1 r = 0 j = 0 - сканирование текста for i = 0 to n - m b = 0 if i < J merge(I, R, J, B) IF B < K + 1 R=I extend(I, J, B)
extend(i, j, b) while (b < K + 1) AND (J - I < M) J = J + 1 IF Yj
Теперь исследуем работу процедуры merge. Как упоминалось ранее, эта процедура находит несовпадения между x(1, j-1) и y(i+1, j) и устанавливает b равным найденному числу. Таким образом, merge оценивает tm[i, 1 ... b] для bk+1, и конечно при этом используется полученная ранее информация. Во-первых, вспомним, что строка r таблицы несовпадений рапортует о несовпадениях, полученных при совмещении начала образца и yr+1, а r+tm[r, k+1] содержит текущий номер самой правой из проверенных на настоящий момент позиций текста. Поэтому несовпадения справа от yi, информация о которых содержится в r-й строке tm, неглупо было бы учитывать при сравнении образца с текстом, начинающимся с yi+1. Подходящими значениями из таблицы несовпадений являются, таким образом, tm[r, q ... k+1], где q – это наименьшее из целых чисел, для которых r+tm[r, q] > i. Однако, следует учитывать тот факт, что эти несовпадения соответствуют началу образца, выравниваемому с yr+1, в то время как текущая позиция образца выровнена с yi+1 – разница в i - r мест.
Вторым источником используемой в merge информации является, таким образом, предварительно вычисленная таблица pm несовпадений, дающая позиции несовпадения образца с самим собой при различных сдвигах. Строка i массива pm[1…m-1, 1 ... 2k+1] содержит позиции внутри x первых 2k+1 несовпадений между подстроками x(1, m-i) и x(i+1, m), то есть перекрывающимися порциями двух копий шаблона для соответствующего сдвига i. Таким образом, если pm[i, u] = s, то xi+sxs, и это u-е несовпадение между x(1, m-i) и x(i+1, m) слева направо. Если число c несовпадений между этими строками меньше 2k+1, то, начиная с c+1, элементы i-й строки равны m+1, значению по умолчанию, то есть:
pm[i, c+1] = pm[i, c+2] = … = pm[i, 2k+1] = m+1
Таким образом, для merge интерес представляет строка i - r таблицы несовпадений, причем используются значения pm[i-r, 1…t], где t – самое правое несовпадение в pm[i-r, 1…2k+1], такое, что pm[i-r, t] < j-i+1, так как требуются только несовпадения в подстроке x(1, j-i).
Чтобы понять, как упомянутая информация может использоваться в процедуре merge, рассмотрим в тексте позицию p, находящуюся в соответствующем диапазоне, i+1pj. Позиция p может удовлетворять или не удовлетворять любому из приведенных ниже условий.
A: когда символы x1 и yr+1 совмещены, позиция p в тексте соответствует предварительно выявленному несовпадению между образцом и текстом, то есть ypxp-r, и это несовпадение номер v, где qvk+1, то есть p - r = tm[r, v].
B: для двух копий образца, со сдвигом относительно друг друга i - r, совмещенных с текстом так, что их начальные символы лежат, соответственно, над yr+1 и yi+1, позиция p соответствует несовпадению между двумя шаблонами, то есть xp-rxp-i. Это u-е несовпадение при этом сдвиге, где 1ut, то есть p-i = pm[i-r, u].
Вспомним, что нас интересует, совпадает ли символ текста в позиции p с соответствующими символом образца, когда x1 совмещен с yi+1, то есть верно ли, что yp = xp-i. Рассмотрим этот вопрос при разных комбинациях указанных выше условий.
Случай 1: не выполняется ни условие A, ни условие B. То есть, yp = xp-r и xp-r = xp-i, откуда yp = xp-i. Нет необходимости сравнивать символ текста с символом шаблона, так как ясно, что в этой позиции они совпадают.
Случай 2: выполняется только одно из условий, то есть либо условие A, либо условие B, но не оба сразу. В любом случае ypxp-i. Если лишь условие A истинно, то ypxp-r и xp-r = xp-i, откуда ypxp-i. С другой стороны, если выполнено только условие B, то yp = xp-r и xp-rxp-i, и опять, ypxp-i. Как и в предыдущем случае, нет необходимости сравнивать символ текста с символом шаблона, так как известно, что они не совпадают.
Случай 3: выполняются оба условия – и условие A, и условие B. В этом случае мы ничего не можем сказать о том, совпадают ли символы yp и xp-i, поэтому их надо сравнить.
В случае 2, или если в случае 3 выявлено несовпадение символов, необходимо увеличить количество несовпадений символов b на единицу и обновить tm[i, b] в процедуре merge.
Теперь опишем процедуру merge, представленную на рисунке 4.27. Как упоминалось ранее, соответствующими значениями таблицы для merge являются tm[i-r, 1…t] и tm[r, q…k+1]. Переменные u и v в начале устанавливаются равными индексам первых элементов этих двух векторов, соответственно, и последовательно увеличиваются соответственно векторным компонентам.
Условия окончания работы процедуры следующие. Во первых, если b = k+1, то для случая, когда шаблон расположен относительно текста так, что x1 совмещен с yi+1, обнаружено k+1 несовпадение, поэтому из процедуры можно выйти. Во вторых, вспомним, что самая правая из интересующих нас позиций в merge, а именно, j, равна r+tm[r, k+1], если v = k+2, поэтому tm[r, k+1] будет уже использовано для предыдущего значения v, а именно, v = k+1, и поэтому позиция j должна быть пропущена. Следовательно, в этом случае также можно выйти из процедуры. Наконец, процедуру можно прервать, если i+pm[i-r, u] > j и tm[r, v] = m+1. Если выполняется вторая часть этого условия, то r+tm[r, v] равняется j, и соответствует суммам для последующих значений v вплоть до k+1. В этом случае процедура может быть прервана, если выполняется также первая часть приведенного условия, так как она указывает, что позиция текста j фактически пропущена.
Остается показать, что число позиций несовпадений в таблице несовпадений шаблона достаточно для того, чтобы merge нашла все, или, если их больше k+1, первые k+1 несовпадений для y(i+1, j). Это можно показать следующим образом. Условие A выполняется не больше чем для k+1 позиции текста в диапазоне [i+1, j]. Условие B выполняется для некоторого неизвестного числа позиций в этом же интервале. Строка i-r в таблице несовпадений шаблона, tm[i-r, 1 ... 2k+1], содержит не больше чем 2k+1 позиций несовпадений между двумя копиями шаблона, с соответствующим сдвигом i-r. Если pm[i-r, 2k+1]
j - i, то таблица содержит все позиции несовпадения шаблона самим с собой, у которых условие B выполняется для позиций текста в интервале [i+1, j]. С другой стороны, если pm[i-r, 2k+1] < j-i, то таблица может дать 2k+1 позиций текста в диапазоне [i+1, j-1], для которых выполняется условие B. Поскольку j = r+tm[r, k+1], в диапазоне [i+1, j-1] имеется до k позиций текста, для которых выполняется условие A. Таким образом, в худшем случае может быть k позиций, для которых имеет место случай 3, и которые требуется сравнить напрямую. Остается по крайней мере k+1 позиций, удовлетворяющих условию B, но не условию A (случай 2), что является достаточным, чтобы заключить, что для данного положения шаблона относительно текста имеется не меньше k+1 несовпадений между текстом и шаблоном.
Теперь исследуем затраты времени на анализ текста. Если исключить вызовы процедур merge и extend, каждая из n-m+1 итераций цикла анализа текста выполняется за фиксированное время, что дает в общей сложности время O(n). Общее число операций, выполняемых процедурой extend во время вызовов равно O(n), так как она проверяет каждый символ текста не больше одного раза. Процедура merge при каждом вызове обрабатывает вектора pm[i-r, 1 ... 2k+1] и tm[r, 1…k+1], которые в сумме имеют 3k+2 элементов. Время работы merge можно рассчитать, соотнеся операции с фиксированным временем с каждым из этих входов, что дает время счета для каждого вызова, равное O(k). Таким образом, можно видеть, что общее время анализа текста составляет O(nk).
merge(i, r, j, b) u = 1 v = q while (b < K + 1) AND (V < K + 2) AND (I + PM[I - R, U]
Рисунок 4.27: Процедура merge Ландау-Вишкина
- инициализация r = 2l-1 j = 2l-1 - вычисление строк pm в множестве l for i = 2l-1 to 2l - 1 b = 0 if i < J merge(I, R, J, B) IF
r = i extend(i, j, b)
Рисунок 4.28: Предварительная обработка образца Ландау-Вишкина
Теперь осталось только обратиться к вычислению таблицы несовпадений шаблона на стадии предварительных вычислений. Не теряя общности, можно предположить, что m является некоторой степенью 2. В алгоритме предварительной обработки используется разбиение множества {1, 2, ... , m-1} из m-1 строк pm на следующие log2m подмножеств:
{1}, {2, 3}, {4, 5, 6, 7}, ... , {m/2, ... , m-1}
Алгоритм состоит из log2m этапов. На этапе s, где 1slog2m, вычисляются строки pm в множестве s, где множество s – это {2s-1, ... , 2s-1}.
Метод, используемый для вычисления этой таблицы, основан на методе, используемом на стадии анализа текста, алгоритм для этапа s приведен на рисунке 4.28. На стадии s входами для алгоритма анализа образца являются подстроки образца x(1, m-2s-1) и x(2s-1+1, m), которые трактуются здесь, соответственно, как образец и текст, и массив pm[1…2s-1-1, 1…min{2log(m)-s4k+1, m-2s-1}], содержащий выходы предыдущих l - 1 стадий. (Число элементов в строках подмассива будет объяснено позже). Выходы стадии s вводятся в. За исключением стадии log2m, на которой находят до 2k+1 несовпадений, на стадии s для каждой строки pm требуется найти до min{2log(m)-s2k+1, m-2s} несовпадений, а не до k+1, как в алгоритме анализа текста.
Используя аргументы, аналогичные применявшимся при проверке корректности процедуры merge, можно показать, что для нахождения требуемого количества несовпадений на стадии s требуется min{2log(m)-s4k+1, m-2s} позиций, для которых выполняется условие B, и в особом случае, а именно, на стадии log2m, требуется 4k + 1 таких позиций.
На каждой стадии s из log2m стадий анализа шаблона цикл for производит 2s-1 итераций (2s-1i2s - 1). Если не считать время работы процедур merge и extend, каждая итерация требует фиксированного времени. Для всех итераций на шаге s процедуре extend требуется время O(m). Ранее было показано, что время работы merge пропорционально числу искомых несовпадений. Таким образом, каждый вызов merge занимает время 
, что равно 
. Таким образом, общее время для стадии s равно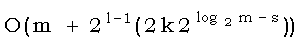 
=O(km). Проведя суммирование по всем стадиям, получаем общее время счета 
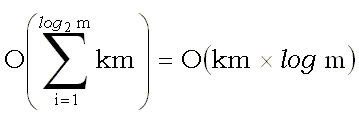. Таким образом, общие затраты времени, включающие предварительную обработку шаблона и анализ текста, равны O(k(n + m log m)).
Алгоритм k различий Ландау-Вишкина [Landau, Vishkin, 1986b, 1989] основан на подходе, близком методу динамического программирования для вычисления расстояния между строками, который предложил Укконен [Ukkonen, 1983, 1985a]. Перед тем, как перейти к этому алгоритму, опишем метод динамического программирования и его адаптацию в стиле Укконена.
Вспомним, что элемент di,j, определяемый (4.9), сообщает расстояние между префиксами с длинами i и j строк, соответственно, x и y. Чтобы решить задачу k различий, матрицу расстояний надо преобразовать таким образом, чтобы di,j представлял минимальное расстояние между x(1, i) и любой подстрокой y, заканчивающейся символом yj (Селлерс, 1980). Для этого достаточно изменить граничные условия (задаваемые (4.12)), на
d0,j = 0 для 0 |
(4.59) |
так как минимальное расстояние между 
и любой подстрокой y равно 0.
Остальная часть матрицы вычисляется как раньше, с использованием цен редактирования расстояния Левенштейна, (4.10), и рекуррентного соотношения для di,j (4.11). По завершении, каждое значение, не превосходящее k, в конечной строке указывает позицию в тексте, в которой заканчивается строка, имеющая не больше k отличий от образца. Это иллюстрируется приведенным ниже примером, в котором показана матрица расстояния для случая x = ABCDE и y = ACEABPCQDEABCR. Из строки 5 этой матрицы можно видеть, что вхождения образца с точностью до 2 отличий, заканчиваются в позициях 3, 10, 13 и 14. Соответствующими подстроками являются ACE, ABPCQDE, ABC и ABCR.
|
|
j |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
i |
|
|
A |
C |
E |
A |
B |
P |
C |
Q |
D |
E |
A |
B |
C |
R |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
A |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
2 |
B |
2 |
1 |
1 |
2 |
1 |
0 |
1 |
2 |
2 |
2 |
2 |
1 |
0 |
1 |
2 |
|
3 |
C |
3 |
2 |
1 |
2 |
2 |
1 |
1 |
1 |
2 |
3 |
3 |
2 |
1 |
3 |
1 |
|
4 |
D |
4 |
3 |
2 |
2 |
3 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
2 |
1 |
1 |
|
5 |
E |
5 |
4 |
3 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
2 |
3 |
3 |
2 |
2 |
Вспомним, что, как описано в алгоритме Укконена, при вычисления расстояний между строками диагонали матрицы можно пронумеровать целыми числами p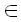
[-m, n], таким образом, чтобы диагональ p состояла из элементов (i, j), у которых j - i = p. Пусть rp,q представляет наибольшую строку i, у которой di,j = q и (i, j) лежит на диагонали p. Таким образом, q – это минимальное число различий между x(1, rp,q) и любой подстрокой текста, заканчивающейся 
, и, кроме того, 
, так как в противном случае требуемым условиям удовлетворяла бы строка rp,q+1, которая больше строки rp,q.
Вернемся к нашему примеру. Ниже представлена диагональ 9 матрицы расстояний. Мы видим, что значениями rp,q в этом случае являются r9,0 = 0, r9,1 = 4 и r9,2 = 5.
|
|
j |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
i |
|
|
A |
C |
E |
A |
B |
P |
C |
Q |
D |
E |
A |
B |
C |
R |
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
1 |
A |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
B |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
C |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
4 |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
5 |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
Значение m в строке rp,q, для qk, указывает, что в тексте имеется вхождение образца с точностью до k отличий, заканчивающееся в ym+p. Таким образом, чтобы решить задачу k различий, достаточно вычислить значения rp,q для qk.
Чтобы объяснить, как можно вычислить значения rp,q, рассмотрим вычисление входов di,j в матрице динамического программирования. Если di,j = q, этот вход находится на диагонали p, и i является наибольшей строкой, удовлетворяющей этим требованиям, тогда по определению rp,q = i. Значение di,j будет выведено по одному из предшествующих ему соседних значений в матрице в соответствии с (4.11). При этом существуют следующие возможности:
yjЕсли последнее появление значения q-1 на диагонали уже найдено, последнее появление значения q на этой диагонали можно найти, проходя через последующие элементы диагонали, пока xi = yj.
Обратите внимание, что первое возможное вхождение образца с точностью до k отличий встречается в позиции текста j = m-k. Эта позиция в строке m лежит на диагонали -k, поэтому диагонали p < -k при вычислениях мы можем не рассматривать. Заметим также, что смежные элементы в матрице могут отличаться только на 0 или 1. Алгоритм, приведенный на рисунке 4.29, можно использовать для вычисления значений rp,q. Начальное значение строки r получают из предыдущих значений rp,q-1, rp-1,q-1 и rp+1,q-1, и последовательно увеличивают на единицу за один раз, пока не будет достигнуто правильное значение rp,q.
То, что алгоритм правильно вычисляет значения rp,q, можно показать следующим образом. Рассмотрим случай, когда q = 0 и вычисляются значения rp,0 (p0). Из граничных условий, начальное значение r равно 0. Цикл while находит, что x(1, rp,0) = y(p+1, p+rp,0) и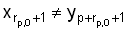 
, устанавливая, таким образом, rp,0 равным правильному значению. Для диагоналей p < 0 правильные значения для rp,|p|-1 и rp,|p|-2 будут установлены во время инициализации. Пусть q = t, и предположим, что все значения rp,t-1 правильны. Рассмотрим вычисление rp,t (p- t). Переменная r устанавливается равной наибольшей строке на диагонали p, такой, что dr,r+p может достичь величины t посредством возможностей 2, 3 или 4, описанных ранее. Цикл while после этого станет перебирать последующие позиции на диагонали, в которых символы шаблона и текста совпадают, пока не придет к правильном значению rp,t.
- инициализация rp,-1 = -1 for 0
Алгоритм вычисляет значения rp,t на n+k+1 диагоналях. Для каждой диагонали переменной строки r можно присвоить не больше m различных значений, что приводит ко времени вычислений O(mn). Таким образом, временные затраты те же, что и у прямого метода динамического программирования, описанного ранее. Однако, теперь мы покажем, как структуру этого метода можно использовать для разработки более эффективного алгоритма.
Улучшение эффективности достигается за счет изменения метода вычисления rp,q. В описанном выше методе переменная r последовательно увеличивается на единичных шагах, пока не будет достигнуто правильное значение rp,q. Однако, благодаря подходящим предварительным вычислениям, значение rp,q можно находить за фиксированное время. Как это сделать, мы расскажем позже, однако сначала рассмотрим требуемые для этого предварительные вычисления.
Стадия предварительных вычислений включает построение так называемого суффиксного дерева, которое можно описать следующим образом. Рассмотрим строку s = s(1, q), где sq = $ – маркер конца, не являющийся частью алфавита, над которым построена строка s(1, q-1). Каждый суффикс s(i, q), 1iq, строки s определяет один из листьев суффиксного дерева для s. Все ребра в дереве направлены от корня, и количество выходящих из каждого узла либо равно нулю (у листьев), либо 2. Если s(i, i+p) – самый длинный общий префикс двух суффиксов s(i, q) и s(j, q), то есть s(i, i+p) = s(j, j+p) и si+p+1sj+p+1, то s(i, i+p) определяет внутренний узел дерева. Два узла, представляющих подстроку b и соответствующий префикс из нее a, соединены ребром только в том случае, если не существует узла, представляющего подстроку c, такого, что c является префиксом b и a является префиксом c. Прерывающий символ $ используется для того, чтобы разделять в дереве суффиксы s(i, q-1) и s(j, q-1), когда один из них является префиксом другого. Обратите внимание, что суффиксное дерево для данной строки уникально с точностью до изоморфизма графов. Структура данных суффиксных деревьев более подробно рассматривается в последующих разделах этой главы.
В качестве примера ниже приведено суффиксное дерево для строки EWEW$, в котором каждый узел помечен определяющей его подстрокой и номером в скобках.
корень --------------------------- (1) $ | | | | | ------------- (2) W ---------- (4) W$ | | | | | ----------- (5) WEW$ | | --------------- (3) EW -------- (6) EW$ | | ------------ (7) EWEW$
При построении дерева подстрока, определяющая конкретный узел, может быть представлена своей длиной и начальной позицией в строке. Эти значения для данного суффиксного дерева приведены ниже, где индексы представляют соответствующий номер узла.
start1 = 5 lenght1 = 1 start2 = 4 lenght2 = 1 start3 = 3 lenght3 = 2 start5 = 2 lenght5 = 4 start6 = 3 lenght6 = 3 start7 = 1 length7 = 5
На этапе предварительной обработки, суффиксное дерево строки y#x$, где # и $ – символы, не принадлежащие алфавиту, над которыми построены строки x и y, строится с помощью алгоритма Вейнера [Weiner, 1973] (который подробно описан Ченом и Сейферасом [Chen, Seiferas, 1985). Этот алгоритм требует линейных затрат памяти, и, для алфавита фиксированного размера, линейного времени. Для неограниченных алфавитов этот алфавит можно преобразовать, так что он будет выполняться за время O(n log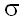
), где 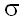– число различающихся символов образца. Стадия предварительной обработки требует время O(n) и O(n log m) для постоянного и неограниченного алфавитов, соответственно. Альтернативные способы предварительной обработки с использованием суффиксных деревьев рассматривались Галилом и Джанкарло (1988).
Теперь можно модифицировать алгоритм, приведенный на рисунке 4.29, чтобы воспользоваться преимуществами вышеуказанной предварительной обработки. Непосредственно перед циклом while для диагонали p, r было присвоено значение, такое, чтобы x(1, r) сопоставлялось с точностью до k различий с некоторой подстрокой текста, заканчивающейся yr+p. Тогда функция цикла while находит максимальное значение, назовем его h, для которого x(r+1, r+h) = y(r+p+1, r+p+h). Это эквивалентно нахождению длины самого длинного общего префикса суффиксов x(r+1, m)$ и y(r+p+1,n)#x$ предварительно вычисленной конкатенированной строки. Символ # используется для предотвращения ситуаций, в которых может ошибочно рассматриваться префикс, состоящий из символов как y, так и x. Если lca(r,p) определяется как самый низкий общий предок (LCA) в суффиксном дереве с листьями, определенными вышеуказанными суффиксами, нужное значение h задается lengthlca(r,p). Таким образом, алгоритм самого низкого общего предка Харела и Тарьяна [Harel, Tarjan, 1984] или Шибера и Вишкина [Schieber, Vishkin, 1988] может использоваться в алгоритме k различий в качестве средства, альтернативного выводу длин нужных сопоставляемых подстрок.
Суффиксное дерево имеет O(n) узлов. Для поддержки определения самого низкого общего предка за линейное время, алгоритмам LCA (самого низкого общего предка) требуется преобразование дерева, проводимое за линейное время. Как упоминалось ранее, значения rp,q вычисляются на n+k+1 диагоналях. Более того, для каждой диагонали надо вычислить k+1 таких значений, что в общей сложности дает O(kn) запросов. Эти вычисления с временем O(kn) дают наибольший вклад в вычисление значений rp,q. Таким образом, общее время прогона для этого алгоритма k различий составляет O(kn) для алфавитов фиксированного размера, и O(n
log(m) +kn) для неограниченных алфавитов.
Кроме того, Ландау и Вишкин [Landau,Vishkin, 1986b, 1989] разработали параллельную версию вышеприведенного алгоритма. Суффиксное дерево может быть вычислено за время O(log n) с использованием n процессоров (Ландау, Шибер и Вишкин [Landau, Schieber, Vishkin, 1987]; Апостолико et al. [Apostolico et al., 1988]). Параллельный алгоритм Шибера и Вишкина может использоваться для предварительной обработки дерева за время O(log n) с использованием n/log n процессоров, при условии, что отдельный процессор выполняет последовательный запрос самого низкого общего предка за время O(1). Таким образом, использование n+k+1 процессоров позволяет выполнять все требуемые запросы самого низкого общего предка за время O(k), – граница, которая также может быть достигнута моделированием алгоритма на n процессорах. Итак, общее требуемое время равно O(log n+k) для n процессоров. Кроме того, Ландау и Вишкин обсуждают, как геометрическая декомпозиция задачи может привести к адаптации алгоритма, по прежнему требующей n процессоров, но выполняющейся за время O(log m + k).
