





|

 |
В методе динамического программирования последовательно, по предыдущим значениям, вычисляются расстояния между все более и более длинными префиксами двух строк – до получения окончательного результата. Опишем этот процесс более подробно.
Пусть di,j есть расстояние между префиксами строк x и y, длины которых равны, соответственно, i и j, то есть
| (4.9) |
Цену преобразования символа a в символ b обозначим через w(a,b). Таким образом, w(a,b) – это цена замены одного символа на другой, когда a b, w(a,
b, w(a, ) – цена удаления a, а w(
) – цена удаления a, а w( , b) – цена вставки b. Заметим, что в случае, когда выполнены нижеследующие условия, d является расстоянием Левенштейна:
, b) – цена вставки b. Заметим, что в случае, когда выполнены нижеследующие условия, d является расстоянием Левенштейна:
 ) = 1 ) = 1
w(  , b) = 1 , b) = 1
w(a, b) = 1, если a  b, b,
w(a, b) = 0, если a=b |
|
В процессе вычислений значения di,j записываются в массив (m+1) (n+1), а вычисляются они с помощью следующего рекуррентного соотношения.
(n+1), а вычисляются они с помощью следующего рекуррентного соотношения.
 ), di,j-1 + w( ), di,j-1 + w( , yj), di-1,j-1 + w(xi, yi)} , yj), di-1,j-1 + w(xi, yi)}
|
(4.11) |
Оно выводится следующим образом. Если предположить, что известна цена преобразования x(1, i-1) в y(1, j), то цену преобразования x(1, i) в y(1,j) мы получим, добавив к ней цену удаления xi. Аналогично, цену преобразования x(1, i) в y(1, j) можно получить, прибавив цену вставки yj к цене преобразования x(1, i) в y(1, j-1). Наконец, зная цену преобразования x(1, i-1) в y(1, j-1), цену преобразования x(1, i) в y(1, j) мы получим, прибавив к ней цену замены xi на yj. Вспомним, что расстояние di,j является минимальной ценой преобразования x(1,j) в y(1,j), поэтому из трех указанных выше операций надо выбрать самую дешевую.
Перед тем, как начать вычислять di,j, надо установить граничные значения массива. Что касается первого столбца массива, то значение di,0 равно сумме цен удаления первых i символов x. Аналогично, значения d0,j первой строки задаются суммой цен вставки первых j символов y. Итак, имеем следующее:
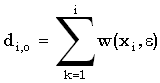 для 1 для 1 i i m m
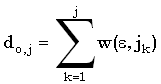 для 1 для 1 j j n n |
|
Для расстояния Левенштейна di,0 = i и d0,j = j. Ниже приведен массив, полученный при вычислении расстояния Левенштейна между строками preterit и zeitgeist. Из него видно, что расстояние между этими строками, то есть d8,9, равно 6.
|
|
j |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
i |
|
|
z |
e |
i |
t |
g |
e |
i |
s |
t |
|
0 |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
p |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
r |
2 |
2 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
3 |
e |
3 |
3 |
2 |
3 |
4 |
5 |
5 |
6 |
7 |
8 |
|
4 |
t |
4 |
4 |
3 |
3 |
3 |
4 |
5 |
6 |
7 |
7 |
|
5 |
e |
5 |
5 |
4 |
4 |
4 |
4 |
4 |
5 |
6 |
7 |
|
6 |
r |
6 |
6 |
5 |
5 |
5 |
5 |
5 |
5 |
6 |
7 |
|
7 |
i |
7 |
7 |
6 |
5 |
6 |
6 |
6 |
5 |
6 |
7 |
|
8 |
t |
8 |
8 |
7 |
6 |
5 |
6 |
7 |
6 |
6 |
6 |
Алгоритм вычисления массива расстояний, разработанный Вагнером и Фишером (Wagner, Fisher), приведен на рисунке 4.10. Можно видеть, что стадия инициализации границ включает 1+m+n, а основной цикл повторяется mn раз. Таким образом, временная сложность этого алгоритма есть O(mn).
- инициализация границ массива d0,0 = 0 for i = 1 to m di,0 = di-1,0 + w(xi,) for j = 1 to n d0,j = d0,j-1 + w(
,yj) - вычисление di,j for i = 1 to m for j = 1 to n di,j = min{di-1,j + w(xi,
), di,j-1 + w(
,yj), di-1,j-1 + w(xi,yj)}
Рис. 4.10. Вычисление расстояния между строками по Вагнеру и Фишеру
Последовательность операций редактирования для преобразования x в y можно получить с помощью структуры, называемой след. След из x в y можно описать как соединение символов строки x с символами помещенной под ней строки y ребрами, причем каждый из символов соприкасается не больше чем с одним ребром, и никакие два ребра не пересекаются. Представляя ребро из xi в yj как упорядоченной парой целых чисел (i, j), след из x в y можно формально определить как множество упорядоченных пар, удовлетворяющих следующим условиям:
 i i m, 1 m, 1 j j n n |
(4.13) |
i1  i2 и j1 i2 и j1 j2, i1 < i2 j2, i1 < i2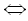 j1 < j2 j1 < j2 |
Последовательность операций редактирования можно получить из следа следующим образом. Все не касающиеся ребер символы x надо удалить, а аналогичные символы y вставить. Для каждого ребра (i, j) в следе, xi заменить на yj, если xi yj, если же xi = yj, то редактирование не требуется. Вернемся к предыдущему примеру: вот как выглядит след с наименьшей ценой от preterit к zeitgeist.
yj, если же xi = yj, то редактирование не требуется. Вернемся к предыдущему примеру: вот как выглядит след с наименьшей ценой от preterit к zeitgeist.
i 1 2 3 4 5 6 7 8
xi p r e t e r i t
| / | \ | \
yj z e i t g e i s t
j 1 2 3 4 5 6 7 8 9
След наименьшей цены, и, таким образом, последовательность операций редактирования наименьшей цены, переводящую x в y, можно получить из заполненного массива расстояний. Алгоритм для выдачи упорядоченных пар следа вы найдете на рисунке 4.11. Процедура начинает работу с dm,n, и идет обратно, пока оба индекса i и j больше 0. Надо определить, по которому из соседей было выведено di,j, и перейти к этой позиции в массиве. Если di,j выведено из di-1,j-1, то выходом будет упорядоченная пара (i,j), соответствующая ребру в следе, то есть замене или сопоставлению, в зависимости от того, равны xi и yj или нет. Если di,j выведено из di-1,j или di,j-1, ничего не выдается, так как удаление и вставка соответствуют символам, не соприкасающимся с ребрами. Так как при каждом проходе цикла уменьшается либо i, либо j, либо оба индекса, максимальное число итераций равно m+n. Таким образом, след наименьшей цены определяется за время O(m+n).
i = m j = n while(i > 0) and (j > 0) if di,j = di-1,j + w(xi,) i = i - 1 else if di,j = di,j-1 + w(
,yj) j = j - 1 else print('(i,j)') i = i - 1 j = j - 1
Для предыдущего примера данная процедура дает следующий след T (в порядке, обратном тому, в котором эти пары выдаются алгоритмом).
T = {(1,1), (3,2), (4,4), (5,6), (7,7), (8,9)}
Теперь совершенно очевидно, как получить lcs(x,y) по следу наименьшей цены из x в y. Компонентами lcs(x, y) являются символы xi, или, что эквивалентно, символы yj, такие, что (i, j)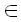 T и xi = yj. Таким образом, для нашего примера мы имеем:
T и xi = yj. Таким образом, для нашего примера мы имеем:
lcs(x, y) = x3x4x5x7x8 = y2y4y6y7y9 = eteit
И наконец, следует упомянуть, что, как указывают Вагнер и Фишер, в некоторых приложениях, скажем, при проверке правописания, может быть полезна весовая функция цены редактирования a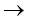 b, w(a,b), зависящая от символов a и b. Например, при стандартной клавиатуре qwerty букву e легче перепутать с w, чем с p. Согласно этому критерию wast, например, будет ближе к east чем к past.
b, w(a,b), зависящая от символов a и b. Например, при стандартной клавиатуре qwerty букву e легче перепутать с w, чем с p. Согласно этому критерию wast, например, будет ближе к east чем к past.
При рассмотрении массива расстояний из приведенного выше метода становится очевидно, что при подходе Вагнера-Фишера требования к памяти равны O(mn). Чтобы избежать проблем с памятью при работе с длинными строками, Хиршберг разработал линейную относительно затрат памяти версию этого алгоритма.
Цель Хиршберга состояла в том, чтобы найти lcs(x,y) для строк x и y. Поэтому вместо расстояний между строками определялись длины самых длинных общих подпоследовательностей у все более и более длинных префиксов. Обозначим их как li,j, то есть:
| (4.14) |
Для данной метрики существует фиксированная взаимосвязь между li,j и di,j. Рассмотрим, например, расстояние редактирование, определяемое следующим ценовыми весами.
 ) = 1 ) = 1 |
(4.15) |
 ,b) = 2, если a ,b) = 2, если a b и 0 в противном случае b и 0 в противном случае
|
Из следа минимальной цены из x в y можно видеть, что расстояние редактирования d(x, y) связано с |lcs(x,y)| выведенным ниже соотношением, где del, ins и sub являются, соответственно, количествами удалений, вставок и замен символов.
= m - (|lcs(x,y)| + sub) + n - (|lcs(x,y)| + sub) + 2sub = m + n - 2 |lcs(x,y)| |
(4.16) |
Отсюда получаем взаимосвязь между li,j и di,j:
li,j = (i + j - di,j)/2 |
(4.17) |
С помощью этого преобразования процедуру динамического программирования для li,j можно вывести из аналогичной процедуры для di,j, см. рисунок 4.12. Так как длина lcs любой строки и пустой равна 0, значения границ массива задаются как li,0 = l0,j = 0. Как и в случае с di,j, значения li,j строятся по предыдущим результатам. В позиции (i,j), то есть когда рассматриваются префиксы x(1,i) и y(1,j), если xi = yj, мы получаем новую lcs, присоединяя этот символ к текущей lcs префиксов x(1, i - 1) и y(1, j - 1), откуда li,j = li-1,j-1 +1. Иначе длина текущей lcs просто равна максимальному из предыдущих соседних значений.
- инициализация границ массива l0,0 = 0 for i = 1 to m li,0 = 0 for j = 1 to n l0,j = 0 - вычисление li,j for i = 1 to m for j = 1 to n if xi = yj li,j = li-1,j-1 + 1 else li,j = max{li-1,j, li,j-1}
Рисунок 4.12: Вычисление |lcs(x,y)|
Затраты памяти можно сократить, если обратить внимание, что для вычисления строки i требуется только строка i-1. Это соображение используется в алгоритме, приведенном на рисунке 4.13. Он выдает вектор ll, где llj = lm,j. Используется массив h длины 2(n+1), в котором строки 0 и 1 выступают в качестве строк i-1 и i массива l, соответственно. Поэтому перед вычислением каждой новой ‘строки i’ строка 1 сдвигается вверх на место строки 0.
Рисунок 4.13: Вычисление |lcs(x,y)| с сокращенными затратами памятиlcs_lengh(m, n, x, y, ll) - инициализация for j = 0 to n h1,j = 0 - вычисление h1,j for i = 1 to m - сдвиг строки вверх for j = 0 to n h0,j = h1,j for j = 1 to n if xi = yj h1,j = h0,1 + 1 else h1,j = max{h1,j-1, h0,j} - копирование результата в выходной вектор for j = 0 to n llj = h1,j
Как и раньше, инструкция if исполняется ровно mn раз, что дает временную сложность O(mn). Входной и выходной массивы требуют m+n+(n+1) ячеек, плюс 2(n+1) ячеек, выделенных для массива h. Поэтому пространственная сложность является линейной по m и n, то есть O(m+n). Этот метод можно использовать для определения lcs(x,y) с линейными затратами памяти, как описано ниже.
Основная идея состоит в том, чтобы рекурсивно делить строку x пополам, и для каждой половины, x1 и x2, находить соответствующие префикс и суффикс, y1 и y2 строки y, такие, что lcs для x1 и y1, соединенные с lcs для x2 и y2, равны lcs полных строк x и y, то есть:
 lcs(x2,y2) = lcs(x,y) lcs(x2,y2) = lcs(x,y) |
(4.18) |
Таким образом, задачу можно рекурсивно разбивать на подзадачи, до сведения их к тривиальным.
Обозначим длину lcs суффиксов x(i+1, m) и y(j+1, n) как 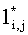 , то есть
, то есть
| (4.19) |
Для 0 j
j n значения li,j являются длинами lcs префикса x(1, i) и различных префиксов y. Аналогично, для 0
n значения li,j являются длинами lcs префикса x(1, i) и различных префиксов y. Аналогично, для 0 j
j n значения
n значения 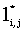 являются длинами lcs обращенного суффикса xR(m, i + 1) и различных префиксов обращенной строки yR. Следующая теорема позволяет находить подходящий префикс и суффикс y, когда x разделена пополам, то есть когда i берется равным
являются длинами lcs обращенного суффикса xR(m, i + 1) и различных префиксов обращенной строки yR. Следующая теорема позволяет находить подходящий префикс и суффикс y, когда x разделена пополам, то есть когда i берется равным 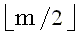 . Теорема гласит, что если x произвольным образом разделить на две части, то максимальное по всем разбиениям y надвое значение суммы длин lcs первых и вторых частей x и y равно длине lcs полных строк x и y.
. Теорема гласит, что если x произвольным образом разделить на две части, то максимальное по всем разбиениям y надвое значение суммы длин lcs первых и вторых частей x и y равно длине lcs полных строк x и y.
Теорема
Определим Mi формулой
| (4.20) |
Тогда
 i i m m |
(4.21) |
Доказательство
Пусть
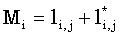 для j = j0 для j = j0 |
(4.22) |
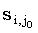 - произвольная lcs(x(1, i), y(1,j0)) - произвольная lcs(x(1, i), y(1,j0)) |
(4.23) |
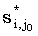 - произвольная lcs(x(i + 1, m), y(j0 + 1, n)) - произвольная lcs(x(i + 1, m), y(j0 + 1, n)) |
(4.24) |
тогда 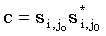 является общей подпоследовательностью x и y, и ее длина равна M. Таким образом,
является общей подпоследовательностью x и y, и ее длина равна M. Таким образом,
| (4.25) |
Пусть sm,n – произвольная lcs(x,y), тогда sm,n является подпоследовательностью y, равной s1 s2, где s1 – это подпоследовательность x(1,i), а s2 – подпоследовательность x(i+1,m). Таким образом, существует значение j1, такое, что s2 является подпоследовательностью y(1, j1), а s2 – подпоследовательностью y(j1+1, n). Длины s1 и s2 удовлетворяют следующим условиям:
s2, где s1 – это подпоследовательность x(1,i), а s2 – подпоследовательность x(i+1,m). Таким образом, существует значение j1, такое, что s2 является подпоследовательностью y(1, j1), а s2 – подпоследовательностью y(j1+1, n). Длины s1 и s2 удовлетворяют следующим условиям:
 |lcs(x(1, i), y(1, j1))| |lcs(x(1, i), y(1, j1))|
 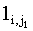 согласно (4.14) согласно (4.14) |
(4.26) |
|s2| |
(4.27) |
Таким образом,
= |s1| + |s2| 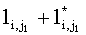 согласно (4.26) и (4.27) согласно (4.26) и (4.27)
 Mi согласно (4.20) Mi согласно (4.20) |
|
Из неравенств (4.25) и (4.28) получаем
| (4.29) |
что, собственно, и требовалось.
На рисунке 4.14 дан полный алгоритм определения lcs(x,y), использующий приведенную выше теорему. В результате возвращается строка c, равная lcs входных строк x и y. Для тривиальной задачи процедура возвращает пустую строку или односимвольную lcs. В противном случае строка x делится пополам, после чего ищутся длина lcs ее первой половины и префиксов y различной длины, и длина lcs ее второй половины и суффиксов y различной длины. Затем по теореме ищется первая позиция в y, обозначаемая здесь k, такая, что lcs первой половины x и y(1,k) в соединении с lcs второй половины x и y(k+1, n) равна требуемой lcs(x, y). Таким образом, остается только использовать это k в двух рекурсивных вызовах процедуры, чтобы получить требуемые lcs подзадач, и соединить их.
Рисунок 4.14: Вычисление lcs(x,y) по Хиршбергуlcs(m, n, x, y, c) - тривиальный случай if n = 0 c = e else if m = 1 if j, 0
j
n, такое что x1 = y1 c = x1 else c = e - нетривиальный случай, разбиение задачи else i = [m/n] -вычисление li,j и l*i,j для 0
j
n lcs_length(i, n, x(1,i), y(1,n), l1) lcs_length(m-i, n, xR(m, i+1), yR(n,1), l2) найти j, такое, что li,j + l*i,j = lm,n M = max {l1j + l2n-j : 0
j
n} k = min j таких, что l1j + l2n-j = M - решение более простой задачи lcs(i, k, x(1, i), y(1, k), c1) lcs(m - i, n - k, x(i + 1, m), y(k + 1, n), c2) - конкатенация результатов - окончательный результат c = c1
c2
В линейности этого алгоритма можно убедиться следующим образом. Строки x и y можно держать в глобальном хранилище, а параметры подстроки можно передавать как указатели аргументов начала и конца подходящих подстрок. Как было показано, вызовы lcs_length требуют временного хранилища, пропорционального m и n. Не считая рекурсивных вызовов, требования к памяти в процедуре lcs являются постоянными. Можно показать, что всего производится 2m - 1 вызовов lcs. Таким образом, общие требования линейны по m и n, то есть затраты памяти у этого метода определения lcs составляют O(m + n). Хиршберг [Hirschberg, 1975] проанализировал также временные затраты этого алгоритма, и показал, что они равны O(mn).
Метод выделения lcs для двух входных строк x и y Ханта и Шиманского (Hunt, Szymanski) эквивалентен нахождению максимального монотонно возрастающего пути в графе, состоящего из точек (i, j), таких, что xi = yj. Мы опишем этот метод, а затем проиллюстрируем его примером.
Для удобства будем считать, что длины входных строк равны, то есть |x| = |y| = n. Алгоритм легко изменить так, чтобы он подходил и для строк разной длины. Количество упорядоченных пар позиций совпадающих символов x и y, то есть мощность множества {(i,j) : xi = yj}, обозначим r.
Ключевым в методе является массив значений ki,l, определяемых соотношением
| (4.30) |
где li,j определены в (4.14).
Таким образом, значение ki,l дает длину самого короткого префикса y, имеющего общую с префиксом x длины i общую подпоследовательность длины s. Вот пример: если x = preterit и y = zeitgeist, то k5,1 = 2, k5,2 = 4, k5,3 = 6, а k5,4 и k5,5 не определены.
Из того, что ki,s по определению является минимальным значением, следует, что последний символ подпоследовательности длины s, общей для префиксов x(1, i) и y(1, ki,j) равен 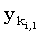 . Итак, длина lcs для x(1, i) и y(1, ki,s-1) равна s - 1. Следовательно, ki,s-1
. Итак, длина lcs для x(1, i) и y(1, ki,s-1) равна s - 1. Следовательно, ki,s-1 ki,s-1, то есть ki,s-1 < ki,s. Отсюда видно, что значения ki,s в каждой строке массива должны монотонно возрастать.
ki,s-1, то есть ki,s-1 < ki,s. Отсюда видно, что значения ki,s в каждой строке массива должны монотонно возрастать.
Значения k можно итеративно вычислять по предыдущим значениям в массиве. В частности, значение ki+1,s может быть выведено по ki,s-1 и ki,s. Перед тем, как продемонстрировать, как это делается, исследуем диапазон значений, в который должно попасть ki+1,s.
Общая для x(1, i) и y(1, ki,s) подпоследовательность длины s будет общей и для x(1, i+1) и y(1, ki,s). Таким образом,
 ki,s ki,s
|
(4.31) |
По определению, x(1, i+1) и y(1, ki+1,s) имеют lcs длины s. Поэтому lcs, построенная для префиксов на один символ более коротких, а именно x(1,i) и y(1, ki+1,s-1), будет короче ее не больше, чем на один символ. Таким образом,
| (4.32) |
Комбинируя (4.31) и (4.32), получаем следующие границы для ki+1,s
ki,s-1 < ki+1,s |
(4.33) |
Правило вычисления ki+1,s по ki,s-1 и ki,s выглядит так:
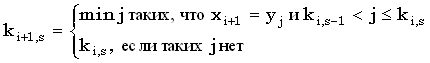 |
(4.34) |
Правильность этого выражения можно доказать следующим образом. Сначала рассмотрим случай, когда подходящих j не существует. Так как ki+1,s является минимальным значением, последняя компонента любой общей для x(1, i+1) и y(1, ki+1,s) подпоследовательности длины s должна быть равна 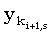 . Из того, что ki+1,s должно лежать внутри задаваемых (4.33) границ, следует, что
. Из того, что ki+1,s должно лежать внутри задаваемых (4.33) границ, следует, что 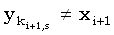 , иначе требуемым значением j было бы ki+1,s. Отсюда, в свою очередь, следует, что эта подпоследовательность длины s является общей для x(1,i) и y(1,ki+1,s), откуда ki,s
, иначе требуемым значением j было бы ki+1,s. Отсюда, в свою очередь, следует, что эта подпоследовательность длины s является общей для x(1,i) и y(1,ki+1,s), откуда ki,s ki+1,s. Комбинируя это с (4.33) получаем, что когда подходящих j не существует, ki+1,s = ki,s.
ki+1,s. Комбинируя это с (4.33) получаем, что когда подходящих j не существует, ki+1,s = ki,s.
Теперь рассмотрим случай, когда существует j, при котором xi+1 = yj и ki,s-1 < j ki,s. Префиксы x(1, i+1) и y(1, j) будут иметь общую подпоследовательность длины s, равную подпоследовательности длины s-1, общей для x(1,i) и y(1, ki,s-1) с присоединенным на конце символом xi+1 (так как xi+1 = yj). Таким образом, ki+1,s
ki,s. Префиксы x(1, i+1) и y(1, j) будут иметь общую подпоследовательность длины s, равную подпоследовательности длины s-1, общей для x(1,i) и y(1, ki,s-1) с присоединенным на конце символом xi+1 (так как xi+1 = yj). Таким образом, ki+1,s j. Теперь осталось узнать, достигнуто ли желаемое равенство, или ki+1,s на самом деле меньше нашего значения j. Предположив последнее, и придя к противоречию, мы тем самым докажем, что выполняется первое. Итак, предположим, что ki+1,s < j. И снова, последним символом общей для x(1, i+1) и y(1, ki+1,s) последовательности длины s должен быть yk+1,s. Так как ki+1,j и j должны лежать в одном интервале (из (4.33) и (4.34)), мы знаем, что yk+1,s
j. Теперь осталось узнать, достигнуто ли желаемое равенство, или ki+1,s на самом деле меньше нашего значения j. Предположив последнее, и придя к противоречию, мы тем самым докажем, что выполняется первое. Итак, предположим, что ki+1,s < j. И снова, последним символом общей для x(1, i+1) и y(1, ki+1,s) последовательности длины s должен быть yk+1,s. Так как ki+1,j и j должны лежать в одном интервале (из (4.33) и (4.34)), мы знаем, что yk+1,s xi+1, поскольку j является минимальным значением в разрешенном диапазоне, при котором yj = xi+1, а мы предполагаем, что ki+1,s < j. Отсюда следует, что x(1,i) и y(1, ki+1,s) также имеют общую подпоследовательность длины s, поэтому ki,s
xi+1, поскольку j является минимальным значением в разрешенном диапазоне, при котором yj = xi+1, а мы предполагаем, что ki+1,s < j. Отсюда следует, что x(1,i) и y(1, ki+1,s) также имеют общую подпоследовательность длины s, поэтому ki,s ki+1,s. Вместе с (4.33) это означает, что ki,s = ki+1,s. Мы предположили, что ki+1,s < j. Таким образом, из (4.34), ki+1,s < ki,s, что противоречит предыдущему результату. Это показывает, что на самом деле j равно требуемому ki+1,s.
ki+1,s. Вместе с (4.33) это означает, что ki,s = ki+1,s. Мы предположили, что ki+1,s < j. Таким образом, из (4.34), ki+1,s < ki,s, что противоречит предыдущему результату. Это показывает, что на самом деле j равно требуемому ki+1,s.
Алгоритм для определения |lcs(x,y)| с помощью ki,s дан на рисунке 4.15. Вектор kk используется как i-я строка массива k. Таким образом, в начале i-й итерации kks = ki-1,s для 0 s
s n, а по завершению итерации, kks = ki,s при 0
n, а по завершению итерации, kks = ki,s при 0 s
s n. Обратите внимание, что kk0 присваивается значение 0, а остальным kk – значение n+1, обозначая неопределенные значения ki,s. Для вычислений требуется только одна строка, так как значения столбцом ниже остаются неизменными или уменьшаются, а значения вдоль строки остаются монотонно возрастающими.
n. Обратите внимание, что kk0 присваивается значение 0, а остальным kk – значение n+1, обозначая неопределенные значения ki,s. Для вычислений требуется только одна строка, так как значения столбцом ниже остаются неизменными или уменьшаются, а значения вдоль строки остаются монотонно возрастающими.
Рис. 4.15: Вычисление |lcs(x,y)| по Ханту-Шиманскому- инициализация kk0 = 0 for s = 1 to n kks = n + 1 - вычисление |lcs(x,y)| for i = 1 to n for j = n downto 1 if xi = yi найти s, для которого kks-1 < J kks kks = j print max s такое, что kks
n + 1
Важно, что в цикле по j идет уменьшение индекса с n до 1. Рассмотрим случай, когда xi совпадает с несколькими символами в y, скажем, 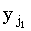 ,
, 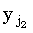 , ... ,
, ... ,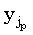 , такими, что ki-1,s-1 < j1 < j2 < ... <jp
, такими, что ki-1,s-1 < j1 < j2 < ... <jp ki-1,s. Из (4.34) можно видеть, что правильным значением ki,s является j1. В процессе итераций, с уменьшением индекса j, ki,s будут присваиваться все меньшие значения jp, jp-1, …, j1, пока в конце не будет присвоено требуемое значение. Если, итерации по j проводить в противоположном направлении, то ki,s сначала будет присвоено правильное значение, однако затем ki,s+1 будет установлено равным j2, ki,s+2 равным j3, и так до ki,s+p-1, что правильным не является.
ki-1,s. Из (4.34) можно видеть, что правильным значением ki,s является j1. В процессе итераций, с уменьшением индекса j, ki,s будут присваиваться все меньшие значения jp, jp-1, …, j1, пока в конце не будет присвоено требуемое значение. Если, итерации по j проводить в противоположном направлении, то ki,s сначала будет присвоено правильное значение, однако затем ki,s+1 будет установлено равным j2, ki,s+2 равным j3, и так до ki,s+p-1, что правильным не является.
В конце процедуры значение |lcs(x,y)| задается максимальным s, для которого определено kn,s. Так как значения kk монотонно возрастают, операция ‘найти’ может быть реализована за время O(log n) путем бинарного поиска. Из того, что инструкция if выполняется ровно n2, следует, что алгоритм выполняется за время O(n2 log n) в худшем случае. Заметим, что в случае строк разной длины граница для инициализации kk и внешнего цикла i будет равна m, а не n, где m < n. Ниже приведены результаты процедуры, где показаны значения ki,s для x = preterit и y = zeitgeist. Из последней строки можно видеть, что |lcs(preterit, zeitgeist)| = 5.
|
i |
s |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
p |
0 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
|
2 |
r |
0 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
|
3 |
e |
0 |
2 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
|
4 |
t |
0 |
2 |
4 |
10 |
10 |
10 |
10 |
10 |
10 |
|
5 |
e |
0 |
2 |
4 |
6 |
10 |
10 |
10 |
10 |
10 |
|
6 |
r |
0 |
2 |
4 |
6 |
10 |
10 |
10 |
10 |
10 |
|
7 |
i |
0 |
2 |
3 |
6 |
7 |
10 |
10 |
10 |
10 |
|
8 |
t |
0 |
2 |
3 |
4 |
7 |
9 |
10 |
10 |
10 |
Исчерпывающий поиск совпадающих символов в приведенном выше алгоритме довольно неэффективен, и его можно избежать, предварительно обработав строки, чтобы получить предварительную запись позиций, в которых они совпадают. Таким образом, можно построить массив указателей matchlist на связанные списки, в котором matchlist[i] дает связанный список позиций j, в которых xi = yj, идущих в порядке убывания. Для повторяющихся экземпляров символа в x можно использовать один и тот же список. Например, списки для x = preterit и y = zeitgeist будут следующими.
matchlist[1] = () matchlist[2] = () matchlist[3] = (6, 2) matchlist[4] = (9, 4) matchlist[5] = matchlist[3] matchlist[6] = () matchlist[7] = (7, 3) matchlist[8] = matchlist[4]
Окончательный алгоритм, включающий это улучшение, а также извлекающий lcs двух строк, представлен на рисунке 4.16. lcs воссоздается с помощью средства поиска с возвратами, используемого при вычислении значений kk. Когда определяется kkj, links устанавливается указывающим на оглавление списка пар (i, j), определяющий общую подпоследовательность длины s. Это реализуется процедурой newnode, создающей узел, содержащий текущую пару (i, j) с указателем на предыдущий узел в списке и возвращающей указатель на только что созданный узел.
Рисунок 4.16: Вычисление lcs(x,y) по Ханту-Шиманскомусоздать списки с использованием указателей for i = 1 to n matchlist[i] = (j1, j2, . . . , jp) такие, что j1 > j2 > … >jp и для 1
q
p - инициализация kk0 = 0 for s = 1 to n kkl = n + 1 link0 = null - вычисление последовательных значений kk for i = 1 to n for j in matchlist[i] найти s такое, что kks-1 < J
kks if j < KKs kks = j links = newnode(i, j, links-1) - выделение lcs в обратном порядке s = max s такое, что kks
n + 1 pointer = links while pointer
null print (i,j) пара указана с помощью pointer продвинуть pointer
Предварительную обработку можно реализовать, сортируя символы каждой строки, записывая их исходные позиции, и сливая затем отсортированные строки для создания списков matchlist. С помощью алгоритма пирамидальной сортировки (heapsort) эту фазу можно выполнить за время O(n log n) с использованием O(n) памяти. Стадия инициализации занимает время O(n). Во время вычисления значений kk внутренний цикл выполняется r раз. Для каждой итерации выполняется бинарный поиск и несколько других операций с фиксированным временем. Таким образом, эта стадия занимает время O(r+r log n) и включает создание r новых узлов. Наконец, фактическое выделение lcs занимает время O(|lcs(x,y)|), которое, разумеется, равно O(n). Таким образом, общие затраты времени и памяти у алгоритмы равны, соответственно, O((r+n)
log n) и включает создание r новых узлов. Наконец, фактическое выделение lcs занимает время O(|lcs(x,y)|), которое, разумеется, равно O(n). Таким образом, общие затраты времени и памяти у алгоритмы равны, соответственно, O((r+n) log n) и O(r+n). И снова, более общий случай строк неравной длины легко реализуется установкой границ для инициализации kk и циклов i равными m вместо n.
log n) и O(r+n). И снова, более общий случай строк неравной длины легко реализуется установкой границ для инициализации kk и циклов i равными m вместо n.
В примере вычисления lcs(preterit, zeitgeist) описанная выше процедура выдает следующий список пар (i, j) для lcs (в обратном порядке):
(8, 9), (7, 7), (5, 6), (4, 4), (3, 2).
Это проиллюстрировано ниже, где узлы указывают точки (i, j), такие что xi = xj. lcs формируется символами в соответствии с заполненными узлами, а именно eteit, и, таким образом, эквивалентна максимальному монотонно возрастающему пути в графе.
|
|
j |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
i |
|
z |
e |
i |
t |
g |
e |
i |
s |
t |
|
1 |
p |
|
|
|
|
|
|
|
|
|
|
2 |
r |
|
|
|
|
|
|
|
|
|
|
3 |
e |
|
 |
|
|
|
 |
|
|
|
|
4 |
t |
|
|
|
 |
|
|
|
|
 |
|
5 |
e |
|
 |
|
|
|
 |
|
|
|
|
6 |
r |
|
|
|
|
|
|
|
|
|
|
7 |
i |
|
|
 |
|
|
|
 |
|
|
|
8 |
t |
|
|
|
 |
|
|
|
|
 |
Апостолико и Гиерра [Apostolico, Guerra, 1987] разработали версию алгоритма Ханта-Шиманского, в которой удалось избежать снижения эффективности последнего до уровня ниже квадратичной в худшем случае. Вариант Апостолико и Гиерра имеет временную сложность O(m log n + t
log n + t log(2mn/t)), что в худшем случае равно O(mn). Здесь t
log(2mn/t)), что в худшем случае равно O(mn). Здесь t r равняется числу доминантных совпадений между строками. k-доминантное совпадение является упорядоченной парой (i, j), такой, что xi = yj, li,j = k, и это первое появление такой точки в подматрице l(1,...,i),(1,...,j) (li,j определяется в (4.14)). Сопоставление (i, j), таким образом, является доминантным, если вхождение в подходящей строке префиксов каждой lcs(x(1,i),y(1,j)) заканчивается символами xi и yj. Вариант Апостолико и Гиерра имеет эффективные средства нахождения доминантных сопоставлений и включает структуры данных, называемые характеристическими деревьями, для представления различных списков, требуемых алгоритмом.
r равняется числу доминантных совпадений между строками. k-доминантное совпадение является упорядоченной парой (i, j), такой, что xi = yj, li,j = k, и это первое появление такой точки в подматрице l(1,...,i),(1,...,j) (li,j определяется в (4.14)). Сопоставление (i, j), таким образом, является доминантным, если вхождение в подходящей строке префиксов каждой lcs(x(1,i),y(1,j)) заканчивается символами xi и yj. Вариант Апостолико и Гиерра имеет эффективные средства нахождения доминантных сопоставлений и включает структуры данных, называемые характеристическими деревьями, для представления различных списков, требуемых алгоритмом.
Верхнюю границу (Джекобсон и Во [Jacobson, Vo, 1992]) для общего числа доминантных совпадений t между двумя строками получают следующим образом. k-доминантные совпадения можно отсортировать в порядке возрастания i, чтобы получить 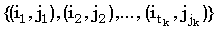 , где tk есть число k-доминантных совпадений, и
, где tk есть число k-доминантных совпадений, и 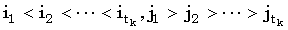 . Так как индексы i и j монотонно убывают и возрастают, соответственно, мы имеем следующие неравенства, где i
. Так как индексы i и j монотонно убывают и возрастают, соответственно, мы имеем следующие неравенства, где i p
p tk:
tk:
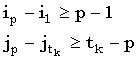 |
(4.35) |
Расстояние редактирования между префиксами x(1, i) и y(1, j) и длина их lcs связаны между собой следующим соотношением:
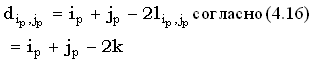 |
(4.36) |
Так как сопоставление (i1, j1) является k-доминантным, мы имеем i1 k, а также, раз
k, а также, раз 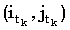 является k-доминантным,
является k-доминантным, 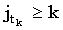 . Объединяя это с (4.36), получаем:
. Объединяя это с (4.36), получаем:
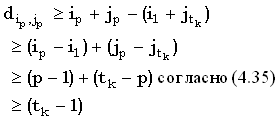 |
(4.37) |
Пусть k'обозначает число, при котором имеется больше всего k-доминантных совпадений. lcs(x,y), построенная только по доминантным совпадениям, должна содержать одно из этих k'-доминантных совпадений, скажем, (ip, jp). Расстояние между полными строками x и y не может быть меньше расстояния между префиксами x(1, i) и y(1, j), то есть:
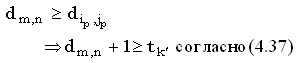 |
(4.38) |
Так как 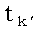 является максимальным числом доминантных совпадений, то есть
является максимальным числом доминантных совпадений, то есть 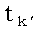
 tl при 1
tl при 1 l
l lm,n, имеем:
lm,n, имеем:
t |
(4.39) |
Комбинируя это с неравенством (4.38), получаем окончательный результат для верхней границы общего числа доминантных совпадений:
 lm,n(dm,n + 1) lm,n(dm,n + 1) |
(4.40) |
Число доминантных совпадений может быть гораздо меньше общего числа совпадений, особенно когда расстояние между строками мало. Граница для t в худшем случае выводится следующим образом. Подставляя вместо dm,n выражение (4.16), получаем следующее:
 lm,n (m + n - 2lm,n + 1) lm,n (m + n - 2lm,n + 1) |
(4.41) |
Для строк равной длины, эта граница достигает максимального значения, равного (2n+1)2/8, при длине lcs, равной (2n+1)/4. Вспомним, что максимальное число совпадений равно n2. Таким образом, можно видеть, что общее число совпадений асимптотически превышает число доминантных совпадений вдвое.
Машек и Патерсон [Masek, Paterson, 1980] применили к процедуре вычисления расстояния между строками Вагнера и Фишера подход ‘четырех русских’ (Арлазарова, Диница, Кронрода и Фараджева [Arlazarov, Dinic, Kronrod, Faradzev, 1970]) и получили алгоритм, выполняющийся за время O(n2/log n). Он и описан ниже.
Матрица расстояний d разбивается на совокупность квадратных подматриц с перекрывающимися крайними векторами. Подматрица (i, j, p) определяется как подматрица размерности (p+1) (p+1), левым верхним элементом которой является di,j. Из определения (4.11) входов матрицы d видно, что значения подматрицы (i, j, p) выводятся из ее соответствующих подстрок x(i+1, i+p) и y(j+1, j+p) и начальных векторов, то есть, ее верхней строки (di,j, di,j+1,… di,j+p) и левого столбца (di,j, di+1,j,...,di+p,j).
(p+1), левым верхним элементом которой является di,j. Из определения (4.11) входов матрицы d видно, что значения подматрицы (i, j, p) выводятся из ее соответствующих подстрок x(i+1, i+p) и y(j+1, j+p) и начальных векторов, то есть, ее верхней строки (di,j, di,j+1,… di,j+p) и левого столбца (di,j, di+1,j,...,di+p,j).
На первом этапе алгоритма вычисляются значения конечных векторов, то есть нижней строки и правого столбца, для всех возможных подматриц (i, j, p) любой матрицы d для данных алфавита и функции цены. Это требует перечисления всех подматриц, для чего нужны списки всех комбинаций возможных подстрок и начальных векторов. Чтобы перечислить все возможные подстроки длины p, мы должны считать, что алфавит конечен. Кроме того, попытки перечислить все возможные начальные вектора могут быть запрещены. Однако, ограничение цен редактирования таким образом, чтобы они стали интегральными множителями некоторых действительных чисел приведет к тому, что они станут всего лишь конечным числом разностей между последовательными значениями d для всех матриц расстояний, использующих один и тот же алфавит и функцию цены. Гораздо практичнее использовать эти разности, чем абсолютные значения. Определяя шаг как разность между любыми двумя горизонтально или вертикально смежными элементами матриц, приходим к следующему следствию правила (4.11) вычисления di,j:
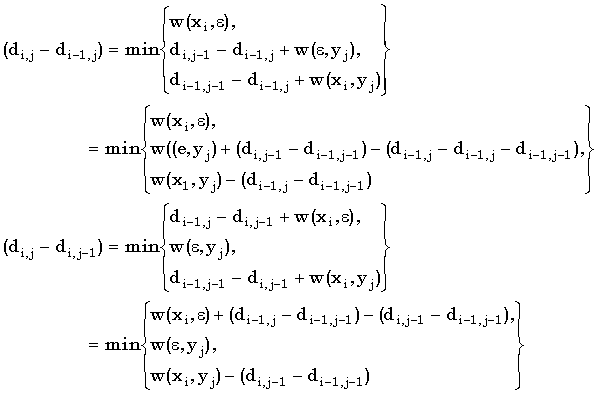 |
(4.42) |
Каждую подматрицу можно, таким образом, вывести по соответствующим подстрокам x(i+1, i+p) и y(j+1, j+p), начальному значению di,j, и начальным векторам – верхней строке (di,j+1 - di,j, ... , di,j+p - di,j+p-1) и первому столбцу (di+1,j - di,j, …, di+p,j - di+p-1,j). Перечисление всех возможных подматриц может быть достигнуто перечислением всех пар строк длины p над конечным алфавитом C, и всех пар векторов шага длины p.
Алгоритм для вычисления всех подматриц приведен на рисунке 4.17. Строки длины p и вектора шага длины p перечисляются в алфавитном порядке, предполагая фиксированное упорядочение на C и на конечном множестве возможных значений шага. Подматрица шага вычисляется для каждой пары строк u и v, и каждой пары векторов начального шага T и L, в соответствии с (4.42). Чтобы облегчить последующее продвижение, процедура store сохраняет векторы конечного шага B и R, подматрицы, определенной u, v. T и L. В процедуре вычисляются две матрицы шагов: V содержит значения вертикального шага, а H – горизонтального.
Рисунок 4.17: Вычисление подматрицы в методе Машека-Патерсонаfor каждой пары строк u, v Cp for каждой пары векторов шага длины p T, L - инициализация векторов начального шага for i = 1 to p Vi,0 = Li H0,i = Ti - вычислить входы матриц шага for i = 1 to p for j = 1 to p
-сохранение результатов R = (V1,p, V2,p, ... , Vp,p) B = (Hp,1, Hp,2, ... , Hp,p) store(R, B, L, T, u, v)
Так как самый внутренний цикл выполняется постоянное время и повторяется ровно p2 раз для каждой пары строк и векторов шага, каждая подматрица вычисляется за время O(p2). Число пар строк длины p над алфавитом  равно
равно  2p. Если s – мощность этого множества возможных значений шага, которое мы будем считать конечным, то всего имеется s2p различных пар векторов шага длины p. Таким образом, всего имеется (s
2p. Если s – мощность этого множества возможных значений шага, которое мы будем считать конечным, то всего имеется s2p различных пар векторов шага длины p. Таким образом, всего имеется (s
 )2p различных подматриц, что в общей сложности дает время обработки O(p2(s
)2p различных подматриц, что в общей сложности дает время обработки O(p2(s
 2p).
2p).
Ранее мы объявили, что при ограничениях на функцию цены множество возможных значений шага является конечным. Рассмотрим это утверждение поближе. Из правила для di,j и граничных условий (4.11)-(4.12) можно видеть, что значения шага ограничены, вне зависимости от того, какие строки рассматриваются:
 (di,j - di-1,j) (di,j - di-1,j) D D
-D  ) : a ) : a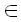 C} C}
I = max{w( |
(4.43) |
Функцию цены называют разреженной, если каждый член множества ценовых весов, а именно {w(a,  ) : a
) : a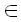
 }
} 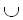 {w(b,
{w(b,  ) : b
) : b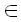
 }
} 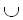 {w(a, b) : a, b
{w(a, b) : a, b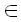
 }, является целым множителем некоторой константы r. Для конечных алфавитов можно показать, что, если функция цены является разреженной, то множество полученных в матрице значений шага является конечным независимо от конкретных строк, что подтверждает сделанное ранее утверждение.
}, является целым множителем некоторой константы r. Для конечных алфавитов можно показать, что, если функция цены является разреженной, то множество полученных в матрице значений шага является конечным независимо от конкретных строк, что подтверждает сделанное ранее утверждение.
Рисунок 4.18: Вычисление расстояния по Машеку-Патерсону- инициализация первого столбца крайних левых подматриц шага for i = 1 to m/p Pi,0 = (w(x(i-1)p+1, e), w(x(i-1)p+2, e), . . . , w(xip, e)) - инициализация верхней строки самых верхних подматриц for j = 1 to n/p Q0,j = (w(e, y(j-1)p+1), w(e, y(j-1)p+2), . . . , w(e, yjp)) - поиск конечных векторов шага для подматриц for i = 1 to m/p for j = 1 to n/p Pi,j, Qi,j = fetch(Pi,j-1, Qi-1,j, x((i - 1)p + 1, ip), y((j-1)p + 1, jp)) - суммирование приращений расстояния для получения dm,n d = 0 for i = 1 to m/p d = d + sum(Pi,0) for j = 1 to n/p d = d + sum(Qm/p,j)
Алгоритм для вычисления расстояния между строками по подматрицам приведен на рисунке 4.18. Пусть m mod p = n mod p = 0, i и j горизонтальный и вертикальный шаги через подматрицы, соответственно. P – это подматрица векторов столбцов подматрицы шага длины p, таких, что Pi,j является самым правым столбцом подматрицы (i, j), совпадающим с левым столбцом подматрицы (i, j + 1), так как смежные подматрицы (p + 1) (p + 1) имеют общий столбец. Аналогично, Q – это матрица векторов строк подматрицы шага длины p, такая, что Qi,j является нижней строкой подматрицы (i, j), совпадающей с верхней строкой подматрицы (i + 1, j). Нулевые столбец и строка, соответственно, P и Q, инициализируются с шагами, соответствующими граничным условиям массива расстояний, задаваемыми (4.12). Процедура fetch возвращает самый правый столбец и нижнюю строку подматрицы (i, j), выбирая вычисленные значения, адресуемые самым левым столбцом и верхней строкой подматрицы вместе с соответствующими подстроками. Наконец, расстояние dm,n между двумя входными строками вычисляется суммированием разностных расстояний вдоль пути из d0,0 в dm,n. Функция sum, применяемая на этом этапе, возвращает сумму своих векторных аргументов.
(p + 1) имеют общий столбец. Аналогично, Q – это матрица векторов строк подматрицы шага длины p, такая, что Qi,j является нижней строкой подматрицы (i, j), совпадающей с верхней строкой подматрицы (i + 1, j). Нулевые столбец и строка, соответственно, P и Q, инициализируются с шагами, соответствующими граничным условиям массива расстояний, задаваемыми (4.12). Процедура fetch возвращает самый правый столбец и нижнюю строку подматрицы (i, j), выбирая вычисленные значения, адресуемые самым левым столбцом и верхней строкой подматрицы вместе с соответствующими подстроками. Наконец, расстояние dm,n между двумя входными строками вычисляется суммированием разностных расстояний вдоль пути из d0,0 в dm,n. Функция sum, применяемая на этом этапе, возвращает сумму своих векторных аргументов.
Инициализация в этом алгоритме выполняется за линейное время, как и конечное суммирование для получения требуемого расстояния. Стадия основных вычислений включает 2mn/p2 просмотров и перекодировок p-мерных векторов, и, таким образом, требует время O(mn/p). Как уже говорилось, предварительные вычисления подматриц требуют время O(p2c2p), где c = s |C|. Если p берется равным min[{logc m, n}/2], то время предварительных вычислений асимптотически меньше времени основных. Таким образом, если учитывать время предварительных вычислений, расстояние определяется за время O(mn/p). Эта граница сохраняется, даже когда m и n не кратны p. В этом случае в конец строк x и y приписывают вспомогательные символы, не встречающиеся них, например,
|C|. Если p берется равным min[{logc m, n}/2], то время предварительных вычислений асимптотически меньше времени основных. Таким образом, если учитывать время предварительных вычислений, расстояние определяется за время O(mn/p). Эта граница сохраняется, даже когда m и n не кратны p. В этом случае в конец строк x и y приписывают вспомогательные символы, не встречающиеся них, например, 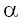 , чтобы длины строк стали интегральными множителями p. Цены редактирования для
, чтобы длины строк стали интегральными множителями p. Цены редактирования для 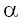 будут следующими:
будут следующими:
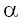 , , ) = 0 ) = 0
 , , 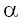 ) = 0 ) = 0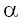 ) = w(a, ) = w(a,  ) ) 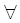 a a 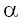 , b) = w( , b) = w( , b)) , b)) 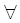 b b |
(4.44) |
Фактическую последовательность редактирования минимальной цены можно получить с помощью метода, близкому к перебору с возвратами Вагнера и Фишера. Требуемые для этого расстояния редактирования можно получить либо перевычисляя подматрицы, через которые проходит путь оптимального редактирования, либо сохраняя заполненные подматрицы во время предварительных вычислений. Последний подход позволяет определять последовательность редактирования по заполненным матрицам P и Q и заранее вычисленным подматрицам за линейное время и требует O(n log2n) памяти для хранения подматриц. Обратите внимание, что матрицы P и Q требуют по (1 + m/p) (1 + n/p)
(1 + n/p) p ячеек каждая, что составляет O(n2/log n). Таким образом, всего при этом методе требуется O(n2/log n) памяти.
p ячеек каждая, что составляет O(n2/log n). Таким образом, всего при этом методе требуется O(n2/log n) памяти.
Этот алгоритм можно также применить к задаче нахождения lcs(x, y), используя функцию цены, задаваемую (4.15). Взаимосвязь между d(x, y) и |l(x, y)|, задаваемая выражением (4.16), позволяет затем вычислить длину lcs за время O(n2 log n). Саму lcs можно получить с помощью метода, похожего на используемый для получения оптимальной последовательности редактирования.
log n). Саму lcs можно получить с помощью метода, похожего на используемый для получения оптимальной последовательности редактирования.
Было показано, что вычисление расстояний между строками с помощью этого метода асимптотически быстрее, чем квадратичный метод Вагнера и Фишера. Однако, на практике реальный выигрыш можно получить только для очень длинных строк. Чтобы проиллюстрировать это, Машек и Патерсон [Masek, Patterson, 1983] вычислили, что для бинарного алфавита и ценовой функции расстояния редактирования, лучшая эффективность достигается только для строк, длина которых превышает 262418.
Метод вычисления расстояния между двумя строками и получения минимальной последовательности операций редактирования Укконена [Ukkonen, 1985] основан на подходе динамического программирования, однако требует O(dm) времени и памяти, где d – это расстояние между строками x и y, а m – меньшая из длин двух строк. Таким образом, этот метод эффективен, когда расстояния между строками малы, то есть когда строки похожи. Основная идея алгоритма состоит в нахождении самого дешевого пути в направленном графе в матрице di,j, в процессе чего избегаются ненужные вычисления di,j.
Как и ранее, будем считать, что m n. Вспомним, что в методе динамического программирования di,j получают, выбирая минимальное из полученных с учетом предварительно вычисленных для соседей значений согласно формуле (4.11). По завершении вычисления dm,n, последовательность операций редактирования минимальной цены получают прослеживанием пути через матрицу, состоящего из переходов, дающих минимальные di,j.
n. Вспомним, что в методе динамического программирования di,j получают, выбирая минимальное из полученных с учетом предварительно вычисленных для соседей значений согласно формуле (4.11). По завершении вычисления dm,n, последовательность операций редактирования минимальной цены получают прослеживанием пути через матрицу, состоящего из переходов, дающих минимальные di,j.
Зависимости между элементами матрицы d можно представить направленными дугами – дуга из (i, j) в (i', j') существует только если di'j' получено из di,j. Полученный в результате граф зависимостей является подграфом графа, состоящего из всех узлов (i, j) и вертикальных, горизонтальных и диагональных (от верхнего левого к нижнему правому) дуг, соединяющих смежные узлы. Эти дуги означают, соответственно, удаления, вставки, а также замены и сопоставления. Поэтому с дугами можно сопоставить цены этих операций, и значение di,j будет, таким образом, задаваться суммой весов по любом пути из (0, 0) в (i, j). Взаимосвязь между дугами и ценами следующая.
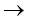 di,j w(xi,
di,j w(xi, )
)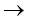 di,j w(
di,j w( , yj)
, yj)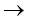 di,j w(xi,yj)
di,j w(xi,yj)Конечные значения на пути из (i,j) в (i', j') в графе зависимостей связаны следующим соотношением, где d – сумма цен всех дуг в пути:
| (4.45) |
Расстояние di,j между двумя строками является, таким образом, минимальной общей ценой пути из d0,0 в dm,n в графе зависимости.
Для определения самого дешевого пути в графе (Ахо, Хопкрофт и Ульман [Aho, Hopcroft, Ullman, 1974]) можно использовать алгоритм Дийкстры (Dijkstra), который сделает это за время O(mn log mn). Однако, топология графа позволяет найти и более эффективное решение, например, метод динамического программирования. Ниже будет показано, как можно сократить число входов массива d, которые нужно вычислить.
Значение dm,n вычисляется только по входам di,j на некотором пути из (0,0) в (m,n). Обратите внимание, что его вычисление требует времени O(n), так как любой такой путь содержит не больше m+n дуг. Рассмотрим задачу выяснения, превосходит ли dm,n некоторый порог, скажем, h. Из 4.11 можно видеть, что значения dij монотонно возрастают вдоль любого пути в графе зависимости. Таким образом, если dm,n h, а некоторое di,j > h, то это di,j не может являться частью пути в (m, n).
h, а некоторое di,j > h, то это di,j не может являться частью пути в (m, n).
Обозначим через wmin минимальную цену всех вставок и удалений, то есть
 ), w( ), w( , a) : a , a) : a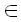  } } |
(4.46) |
для алфавита  . Для ненулевых положительных весов wmin > 0. Кроме того, пронумеруем диагонали матрицы расстояний целыми числами k
. Для ненулевых положительных весов wmin > 0. Кроме того, пронумеруем диагонали матрицы расстояний целыми числами k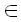 [-m, n] таким образом, чтобы диагональ k состояла из элементов (i, j), у которых j - i = k.
[-m, n] таким образом, чтобы диагональ k состояла из элементов (i, j), у которых j - i = k.
Рассмотрим произвольный путь из (i, j) в (i', j') в графе зависимости. Элемент (i, j) лежит на диагонали k = j - i, а (i', j') – на диагонали k' = j' - i'. Если k' - k 0, то путь содержит не меньше |k' - k| удалений (вертикальных дуг), а если k' - k
0, то путь содержит не меньше |k' - k| удалений (вертикальных дуг), а если k' - k 0, не меньше |k' - k| вставок (горизонтальных дуг). Из (4.45) мы имеем следующее:
0, не меньше |k' - k| вставок (горизонтальных дуг). Из (4.45) мы имеем следующее:
 di,j + |(j' - i') - (j - i)|*wmin di,j + |(j' - i') - (j - i)|*wmin |
(4.47) |
Таким образом, di,j |j - i|*wmin для каждого (i, j) на пути из (0,0) в (m, n). Кроме того, так как di,j
|j - i|*wmin для каждого (i, j) на пути из (0,0) в (m, n). Кроме того, так как di,j dm,n для любого (i, j) в пути, мы имеем следующее:
dm,n для любого (i, j) в пути, мы имеем следующее:
 di,j/wmin di,j/wmin dm,n/wmin dm,n/wmin |
(4.48) |
Для вычисления dm,n достаточно рассмотреть элементы на диагональной ленте dm,n/wmin j - i
j - i dm,n/wmin. На самом деле, эту ленту можно сузить еще больше, что и будет показано ниже.
dm,n/wmin. На самом деле, эту ленту можно сузить еще больше, что и будет показано ниже.
Рассмотрим путь из (0, 0) в (m, n) в графе зависимости. Его можно разложить на два пути: из (0, 0) в (i, j) и из (i, j) в (m, n). Из (4.47) мы имеем следующее:
 d0,0 + |j - i|*wmin + |(n - m) - (j - i)| d0,0 + |j - i|*wmin + |(n - m) - (j - i)| wmin wmin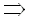 dm,n dm,n  (|j - i| + |(n - m) - (j - i)| (|j - i| + |(n - m) - (j - i)| wmin wmin |
(4.49) |
Рассмотрим два случая: первый, когда j i, а второй, когда j
i, а второй, когда j i. В первом случае (4.49) принимает вид
i. В первом случае (4.49) принимает вид
 (-(j - i) + n - m - (j - i))wmin (-(j - i) + n - m - (j - i))wmin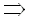 dm,n/wmin - (n - m) dm,n/wmin - (n - m) -2(j - i) -2(j - i) |
(4.50) |
С учетом того, что j - i целое число!!!!!!!!!!!!!!!!Ј 0, отсюда вытекает
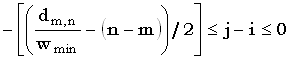 |
(4.51) |
Для случая, когда j i, рассмотрим две возможности, а именно, n - m
i, рассмотрим две возможности, а именно, n - m j - i, и n - m
j - i, и n - m j - i. В первом случае (4.49) принимает вид
j - i. В первом случае (4.49) принимает вид
 (j - i + n - m - (j - i))wmin (j - i + n - m - (j - i))wmin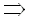 dm,n/wmin dm,n/wmin n - m n - m |
(4.52) |
а во втором
 (j - i + j - i - (n - m))wmin (j - i + j - i - (n - m))wmin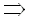 dm,n/wmin - (n - m) dm,n/wmin - (n - m) 2(j - i) - 2(n - m) 2(j - i) - 2(n - m) |
(4.53) |
С учетом того факта, что в данном случае j - i является целым числом  0, получаем
0, получаем
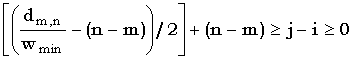 |
(4.54) |
Объединяя (4.51) и (4.54), получаем следующие ограничения на j - i для точек (i, j), лежащих на некотором пути из (0,0) в (m, n) в графе зависимости:
 j - i j - i n - m + p, n - m + p,
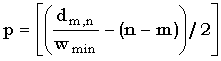 |
(4.55) |
Следствием из (4.55) является то, что для проверки выполнения неравенства d(x, y) h можно ограничиться вычислением di,j, лежащих на ленте между диагоналями -p и n-m+p, где p = [(h/wmin - (n - m))/2].
h можно ограничиться вычислением di,j, лежащих на ленте между диагоналями -p и n-m+p, где p = [(h/wmin - (n - m))/2].
Алгоритм для реализации этого порогового критерия приведен на рисунке (4.19). Проверка возвращает отрицательное значение, если критерий не выполнился, и значение dm,n, если оно меньше или равно пороговому. Критерий не выполняется в тривиальном случае, задаваемом выражением (4.52), так как расстояние должно быть по меньшей мере равно разности длин строк умножить на минимальную стоимость вставок и удалений. В не тривиальном случае вычисляются значения di,j на диагональной ленте, задаваемой (4.55). По завершении этих вычислений окончательное значение dm,n сравнивается с пороговым.
Рисунок 4.19: Пороговый критерий расстояния между строк Укконенаdistance_test(h) if h/wmin < N - M - ТРИВИАЛЬНЫЙ СЛУЧАЙ RETURN(-1) else - ИНИЦИАЛИЗАЦИЯ P = INT((H/Wmin - (n - m))/2) d0,0 = 0 for j = 1 to min{n, n - m + p} d0,j = d0,j-1 + w( , yj) - вычислить dm,n for i = 1 to m for j = max{0, i - p} to min{n, i + n - m + p} if j = 0 di,0 = di-1,0 + w(xi,
) else di,j = min{di-1,j + w(xi,*), di,j-1 + w(
,yj), di-1,j-1 + w(xi,yj)} if dm,n
h return(dm,n) else return(-1)
Рисунок 4.20: Вычисление расстояния между строками Укконенаh = (n - m + 1)wmin while (d = distance_test(h)) < 0 H = 2H
Для каждой из m+1 строк количество вычисляемых элементов матрицы не превосходит n-m+2p+1, что является O(h), как показано ниже.
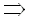 2p 2p h/wmin - (n - m) h/wmin - (n - m)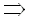 n - m + 2p + 1 n - m + 2p + 1 1 + h/wmin= O(h) 1 + h/wmin= O(h) |
(4.56) |
Таким образом, пороговый критерий выполняется за время O(hm), и требует O(hm) памяти, если сохраняются только значения на диагональной ленте. Обратите внимание, что если требуется только значение расстояния между строками, то требования к памяти можно сократить до O(h) ячеек, так как для вычисления текущей строки требуются только значения предыдущей строки (алгоритм Хиршберга с линейным временем).
Чтобы найти фактическое расстояние между двумя строками, можно вызывать процедуру порогового критерия с последовательно возрастающими значениями h, пока критерий не выполнится. Алгоритм для этого приведен на рисунке 4.20. В начале порогу присваивается минимальное из возможных значений расстояния плюс wmin, которое затем последовательно удваивается. По завершении d равняется расстоянию между двумя строками.
Обозначим начальное пороговое значение h0, следующее, равное 2h0, h1, следующее, равное 22h0, h2, и т.д. Таким образом, r-е значение hr равно 2rh0. Если для определения d(x, y) требуется r вызовов distance_test, то всего требуется время 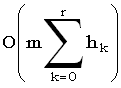 , то есть O(m(2hr - 1)), что равно O(mhr). Однако, так как d > hr/2, общая временная сложность равна O(dm). Фактическая последовательность редактирования может быть вычислена по завершению как в методе Вагнера-Фишера.
, то есть O(m(2hr - 1)), что равно O(mhr). Однако, так как d > hr/2, общая временная сложность равна O(dm). Фактическая последовательность редактирования может быть вычислена по завершению как в методе Вагнера-Фишера.
Укконен рассмотрел также частный случай, когда цены всех операций редактирования равны (то есть вычисление расстояния Левенштейна), для которого можно сократить требования к памяти и применить более эффективный, со временем O(dm), прямой метод вычисления d(x, y).
Ниже описан алгоритм hcs Джекобсона и Во [Jacobson, Vo, 1992], выведенный из алгоритма поиска самой длинной возрастающей подпоследовательности (lis) Робинсона-Шенстеда [Schensted, 1961]. Представленые здесь алгоритмы модифицированы – в них исправлено построение направленных графов, используемых в процедурах.
Прежде всего, вес общей для строк x и y подпоследовательности s можно определить следующим образом:
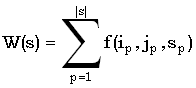 |
(4.57) |
где (ip, jp) – пара сопоставленных символов из x и y, то есть 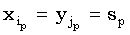 , а f – весовая функция.
, а f – весовая функция.
Для вычисления hcs можно приспособить метод динамического программирования. Обозначим W(hcs(x(1, i), y(1, j))) как Wi,j. Тогда рекуррентное соотношение для Wi,j задается формулой
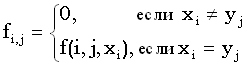 |
(4.58) |
Соотношения следуют из метода вычисления матрицы l. В позиции (i, j), то есть когда рассматриваются префиксы x(1, i) и y(1, j), если xi = yj, новую общую подпоследовательность можно получить добавлением этого символа к текущей общей подпоследовательности строк x(1, i - 1) и y(1, j - 1), а ее вес – добавлением веса этого сопоставления к весу текущей общей подпоследовательности. В противном случае позиция (i, j) не меняет предыдущий результат. Таким образом, вес для позиции (i, j) задается самой тяжелой из предыдущих соседних позиций и, при определенных условиях, новым выведенным весом.
Алгоритм Робинстона-Шенстера для вычисления lis строки y представлен на рисунке 4.21. L – это упорядоченный список пар (a, k), где a – символ строки, а k – его номер в строке. Каждая из следующих операций может быть выполнена за время O(log n), когда L реализуется с помощью сбалансированного дерева.
insert(L, a) - вставить объект a в список L delete(L, a) - удалить объект из списка L next(L, a) - возвратить наименьший из строго больших a объектов в L prev(L, a) - возвратить наибольший из строго меньших a объектов в L max(L) - возвратить наибольший объект в L min(L) - возвратить наименьший объект в L
Когда ничего не определено, процедуры next, prev, max и min возвращают нулевое значение. Операции next(L, null) и prev(L, null) задаются равными, соответственно, min(L) и max(L).
Для каждого символа yj через a обозначим символ в L, после которого можно вставить yj, не нарушая строго возрастающий порядок в этом списке. Элемент, стоящий в L после a при этом заменяется на yj. Направленный граф символов строки создается с помощью массива node (узел). Элементами node являются указатели на узлы, созданные процедурой newnode, и содержащие символ, его номер в строке и адрес предыдущего узла. По завершении lis строки y можно воссоздать обратным перебором в графе - начиная с максимального компонента L.
Рисунок 4.21: Вычисление lis по Робинсону-Шенстеду- инициализация списка L L = null вычисление lis for i = to n (a, k) = prev(L, (yi, 0)) (b, l) = next(L, (a, k)) if b null delete(L, (b, l)) (L, (yi, i)) nodei = newnode((yi, i), nodek)
Обратите внимание, что and в цикле while является условным, т.е. второй операнд вычисляется, только в случае, если первый оказался истинным.- инициализация списка L L = null - вычисление his for i = 1 to n (a, u, k) = prev(L, (yi, 0, 0)) (b, v, l) = next(L, (a, u, k)) while ((b, v, l) null) and (u + f(i, yi)
v) delete(L, (b, v, l)) (b, v, l) = next(L, (b, v, l)) if ((b, v, l) = null) or (yi < B) INSERT(L, (Yi, u + f(i, yi), i)) nodei = newnode((yi, u + f(i, yi), i), nodek)
Для вычисления his необходимо, по мере работы процедуры, прослеживать кумулятивные общие веса his последовательно удлиняющихся префиксов строк. Компонентами L, таким образом, можно сделать тройки (a, u, k), где a – символ входной строки, u – общий вес his, заканчивающейся символом a, а k – номер a в строке. L остается строго монотонным по всем трем своим компонентам. Поэтому порядок в L можно поддерживать соответствующим алфавитному порядку первых элементов пары.
Алгоритм вычисления his, основанный на алгоритме для lis, приведен на рисунке 4.22. Снова a обозначает наибольший из меньших yi символов в L, так что последний можно добавить к любой возрастающей подпоследовательности, заканчивающейся символом a, и опять получить возрастающую подпоследовательность. Если таких a нет, то u берется равным 0. Цикл while обеспечивает поддержание строгой монотонности второго элемента тройки. Затем новая тройка вставляется в список L, если это согласуется со строгим возрастанием первого элемента троек. Массив node применяется для построения связанной структуры для воссоздания фактической his по завершению процесса.
Рассмотрим состояние списка L в конце каждой итерации, обозначаемое Li. Для каждой компоненты (a, u, k) из Li можно воссоздать возрастающую последовательность префикса y(1, i), заканчивающуюся a, путем обратного прохода от символа a в направленном графе. Далее будет показано, что для каждой возрастающей подпоследовательности s(1, k) префикса y(1, i) существует элемент b списка Li, такой, что b sk, т.е. прерывающий возрастающую подпоследовательность в графе, не менее тяжелую, чем s(1, k). Таким образом, максимальный символ Li вместе с графом дают his префикса y(1, i). Следовательно, максимальный элемент L по завершении процесса определяет his для всей строки y.
sk, т.е. прерывающий возрастающую подпоследовательность в графе, не менее тяжелую, чем s(1, k). Таким образом, максимальный символ Li вместе с графом дают his префикса y(1, i). Следовательно, максимальный элемент L по завершении процесса определяет his для всей строки y.
Приведенное выше утверждение очевидно правильно для i = 1. Предположим, что оно справедливо для итерации i - 1, и рассмотрим ситуацию для итерации i. Пусть s(1, k) – это возрастающая подпоследовательность для префикса y(1, i). Из вышеупомянутого, если sk = yi, то в Li-1 имеется элемент b sk-1, определяющий возрастающую подпоследовательность, не менее тяжелую, чем s(1, k - 1). Итак, элемент b не может быть удален из списка на этой итерации, поскольку b < yi. В конце i-й итерации yi либо вставляется в список, либо уже там присутствует. Помня, что кумулятивные веса в L являются строго возрастающими, можно видеть, что возрастающая подпоследовательность, определяемая yi, удовлетворяет сделанному предположению.
sk-1, определяющий возрастающую подпоследовательность, не менее тяжелую, чем s(1, k - 1). Итак, элемент b не может быть удален из списка на этой итерации, поскольку b < yi. В конце i-й итерации yi либо вставляется в список, либо уже там присутствует. Помня, что кумулятивные веса в L являются строго возрастающими, можно видеть, что возрастающая подпоследовательность, определяемая yi, удовлетворяет сделанному предположению.
Теперь перейдем к ситуации, когда sk yi. Здесь имеются две возможности: sk < yi и sk > yi. В первом случае предположение выполняется, так как часть списка, предшествующая yi, не затрагивается i-й итерацией. Остается рассмотреть случай, когда sk > yj. Последовательность s(1, k) тогда должна быть также возрастающей подпоследовательностью y(1, i-1). Таким образом, должна существовать возрастающая подпоследовательность, определяемая некоторым b в Li-1, не менее тяжелая, чем s(1, k). Если b имеется в Li, предположение очевидно выполняется. В противном случае b должен быть исключен из L на i-й итерации, причем взвешивающее условие цикла while гарантирует, что последовательность, определяемая yi, является не менее тяжелой, чем предыдущая, определяемая b. Таким образом, мы показали, что наше предположение справедливо при всех обстоятельствах, поэтому алгоритм корректно вычисляет his входной строки.
yi. Здесь имеются две возможности: sk < yi и sk > yi. В первом случае предположение выполняется, так как часть списка, предшествующая yi, не затрагивается i-й итерацией. Остается рассмотреть случай, когда sk > yj. Последовательность s(1, k) тогда должна быть также возрастающей подпоследовательностью y(1, i-1). Таким образом, должна существовать возрастающая подпоследовательность, определяемая некоторым b в Li-1, не менее тяжелая, чем s(1, k). Если b имеется в Li, предположение очевидно выполняется. В противном случае b должен быть исключен из L на i-й итерации, причем взвешивающее условие цикла while гарантирует, что последовательность, определяемая yi, является не менее тяжелой, чем предыдущая, определяемая b. Таким образом, мы показали, что наше предположение справедливо при всех обстоятельствах, поэтому алгоритм корректно вычисляет his входной строки.
Основной цикл алгоритма повторяется n раз, причем каждая из выполняемых в нем операций требует не больше O(log n) времени. Обратите внимание, что общее количество итераций внутреннего цикла while не превышает n, так как каждый из n элементов y может быть вставлен или удален из списка L не больше одного раза. Таким образом, временная сложность этого алгоритма составляет O(n log n).
i 1 2 3 4 5 6 7 8 9 Yi z e i t g e i s t f(i,yi) 1 1 1 1 1 2 2 1 2 Li (z,1) (e,1) (e,1) (e,1) (e,1) (e,2) (e,2) (e,2) (e,2) (i,2) (i,2) (g,2) (t,3) (i,4) (i,4) (i,4) (t,3) (t,3) (s,5) (s,5) (t,7)
Работу этого метода можно проиллюстрировать следующим примером. Выше приведены компоненты (a, u) троек списка L на каждом шаге i для случая y = zeitgeist. Заметим, что lis в этой строке является eigst. Однако, для первого появления символа в строке веса выбираются равными 1, а для второго – равными 2. При этих условиях возрастающая подпоследовательность eist, использующая вторые e и i, тяжелее, чем lis eigst. По завершении (t, 7), максимальный элемент L, используется для воссоздания пути e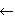 is
is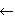 t в направленном графе.
t в направленном графе.
Направленный граф
null <--- (z, 1) null <--- (e, 1) <--- (i, 2) <--- (t, 3) | –---<--- (g, 2) null <--- (e, 2) <--- (i, 4) <--- (s, 5) <--- (t, 7)
Если сопоставления (i, j) между строками x и y записать в порядке возрастания i и в порядке убывания j для равных значений i, то каждая общая подпоследовательность очертит возрастающую подпоследовательность последовательности значений j. И наоборот, общую подпоследовательность можно вывести из возрастающей подпоследовательности значений j. Убывающий порядок j для одинаковых i предотвращает включение в подпоследовательность нескольких символов y, сопоставляемых одному символу x. Ниже приведен пример для строк preterit и zeitgeist. Подчеркнутые символы образуют lis последовательности j, соответствующую lcs этих двух строк.
i 1 2 3 4 5 6 7 8 xi p r e t e r i t - - - - - j 1 2 3 4 5 6 7 8 9 yj z e i t g e i s t - - - - -
Сопоставления
i 3 3 4 4 5 5 7 7 8 8 j 6 2 9 4 6 2 7 3 9 4 - - - -
В приведенном выше упорядочении сопоставлений, соответствующие веса f(i, j, xi) можно приписать значениям j. Реализующий это метод, приведенный на рисунке 4.23, является обобщением алгоритма lcs Ханта-Шиманского. Обратите внимание, что для простоты здесь показаны только компоненты (a, u) троек списка L.
Массив position содержит упорядоченный список позиций вхождения символов в y. Этим он похож на matchlist алгоритма Ханта-Шиманского. Последний давался в порядке убывания, в то время как списки массива positions даются в порядке возрастания. Правильный порядок сопоставлений достигается продвижением назад от позиции j до позиции  для каждого i. К полученной последовательности значений j применяется алгоритм his. Соответствующую hcs(x, y) можно воссоздать после завершения процесса по направленному графу, построение которого в алгоритме также опущено для простоты.
для каждого i. К полученной последовательности значений j применяется алгоритм his. Соответствующую hcs(x, y) можно воссоздать после завершения процесса по направленному графу, построение которого в алгоритме также опущено для простоты.
- построение упорядоченных списков позиций символов в y
for i = 1 to n
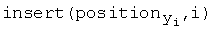 - инициализация списка L
L = null
- вычисление hcs
for i = 1 to n
- инициализация списка L
L = null
- вычисление hcs
for i = 1 to n
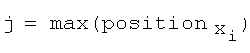 while j
while j null
(a, u) = prev(L, (j, 0))
(b, v) = next(L, (a, u))
while ((b, v)
null
(a, u) = prev(L, (j, 0))
(b, v) = next(L, (a, u))
while ((b, v) null) and (u + f(i, j, xi)
null) and (u + f(i, j, xi) v)
delete(L, (b, v))
if ((b, v) = null) or (j < B)
INSERT(L, (J, U + F(I, J, Xi)))
v)
delete(L, (b, v))
if ((b, v) = null) or (j < B)
INSERT(L, (J, U + F(I, J, Xi)))
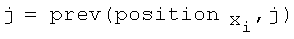
Обратите внимание, что and в цикле while является ‘условным’
Общая длина последовательностей значений j равна числу сопоставлений, r. Время счета зависит также от размера списка L, который ограничен длиной более короткой из двух входных строк. Таким образом, общее время выполнения составляет O((r + m)log n).
Следующий пример иллюстрирует вычисление hcs. Как упоминалось в предыдущей главе, весовая функция минимального расстояния может применяться для указания предпочтений при выборе общих подпоследовательностей для близко выровненных сопоставлений. Рассмотрим пару строк warfare и forewarn. Ниже приведены общие подпоследовательности этой пары вместе с их весами согласно весовой функции минимального расстояния 8 - |i - j|, которая вознаграждает близко выровненные сопоставления. Веса всей lcs даются в скобках.
i 1 2 3 4 5 6 7 xi w a r f a r e yj f o r e w a r n j 1 2 3 4 5 6 7 8 xi w a r w a r w a r i 1 2 3 1 2 6 1 5 6 j 5 6 7 5 6 7 5 6 7 8 - |i - j| 4 4 4 (12) 4 4 7 (15) 4 7 7 (18) xi r a r f a r f r e i 3 5 6 4 5 6 4 6 7 j 3 6 5 1 6 7 1 3 4 8 - |i - j| 8 7 7 (22) 5 7 7 (19) 5 5 5 (15)
Мы видим, что самой тяжелой из lcs является rar. Состояние списка L после каждого этапа i вычисления hcs(warfare, forewarn) для данной взвешивающей функции показано ниже, вместе получившимся направленным графом. И снова для простоты даются только компоненты (a, u).
i 1 2 3 4 5 6 7
xi w a r f a r e
Li (5,4) (5,4) (3,8) (1,5) (1,5) (1,5) (1,5)
(6,8) (7,12) (3,8) (3,8) (3,10) (3,10)
(7,12) (6,15) (6,15) (4,15)
(7,22) (7,22)
Направленный граф
null <--- (5, 4) <--- (6, 8) <--- (7, 12) NULL <--- (3, 8) <--- (6, 15) <--- (7, 22) NULL <--- (1, 5) <--- (3, 10) <--- (4, 15)
По завершении максимальный элемент L, а именно, (7, 22) используется для получения пути 3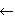 6
6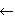 7 из направленного графа значений j в соответствии с подпоследовательностью rar.
7 из направленного графа значений j в соответствии с подпоследовательностью rar.
Частным случаем задачи hcs является случай, когда веса не зависят от позиции, то есть когда f является функцией только символов. Ниже обсуждается алгоритм, позволяющий воспользоваться даваемыми этим частным случаем преимуществами.
Когда весовая функция не зависит от позиции, все веса, соответствующие позициям j в списке  равны. Рассмотрим случай, когда данный j вставляется в список L после a. Вспомним, что значения j из списка позиции обрабатываются в убывающем порядке, поэтому если следующее пробное значение j также больше a, то старое j удаляется из списка, а на его место вставляется новое, так как оба они имеют один и тот же вес. Этого можно избежать, если переходить прямо к наименьшему j в
равны. Рассмотрим случай, когда данный j вставляется в список L после a. Вспомним, что значения j из списка позиции обрабатываются в убывающем порядке, поэтому если следующее пробное значение j также больше a, то старое j удаляется из списка, а на его место вставляется новое, так как оба они имеют один и тот же вес. Этого можно избежать, если переходить прямо к наименьшему j в  , большему a. Таким образом, j можно присвоить значение next(
, большему a. Таким образом, j можно присвоить значение next( , a) после присвоений (a, u) и (b, v).
, a) после присвоений (a, u) и (b, v).
Если j уже присутствует в списке L, то b присваивается значение j. Если вход в L, непосредственно предшествующий j, тот же, что и при вставке j, то алгоритм просто удалит j из L, а затем заново вставит его в ту же точку. Таким образом, когда элемент j вставляется в L, он может быть удален из  во избежание напрасных повторов. Однако, он должен быть восстановлен в своем списке позиции, в случае удаления из списка L или изменения его предшественника в списке L.
во избежание напрасных повторов. Однако, он должен быть восстановлен в своем списке позиции, в случае удаления из списка L или изменения его предшественника в списке L.
- построение упорядоченных списков позиций символов в y for i = 1 to nОбратите внимание, что and в цикле while является ‘условным’- инициализация списка L L = null - вычисление hcs for i = 1 to m
while j
null (a, u) = prev(L, (j, 0)) (b, v) = next(L, (a, u)) j = next(
, a) while ((b, v)
null) and (u + f(xi)
v) delete(L, (b, v)) (b, v) = next(L, (b, v))
insert(L, (j, u + f(xi))) delete(
, j)
И наконец, когда веса не зависят от позиции, условие вставки j в L можно не проверять. Значение b не может быть меньше j, так как a является наибольшим из меньших j элементов списка L. Таким образом, b j. В случае, когда b > j, j можно вставить в L между a и b не нарушая монотонности списка. Если b = j, j можно смело вставлять вместо b, так как их веса одинаковы. Отсюда и видно, что j можно безбоязненно вставлять в L.
j. В случае, когда b > j, j можно вставить в L между a и b не нарушая монотонности списка. Если b = j, j можно смело вставлять вместо b, так как их веса одинаковы. Отсюда и видно, что j можно безбоязненно вставлять в L.
На рисунке 4.24 приведен алгоритм hcs, включающий описанные выше усовершенствования для случая весов, не зависящих от позиции; в алгоритме опять для простоты опущено построение направленного графа и указаны только пары (a, u) триплетов списка L. Если веса всех символов алфавита равны, этот алгоритм превращается в алгоритм lcs Апостолико-Гиерра.